Оглавление:
Примеры практического применения уравнения Д. Бернулли
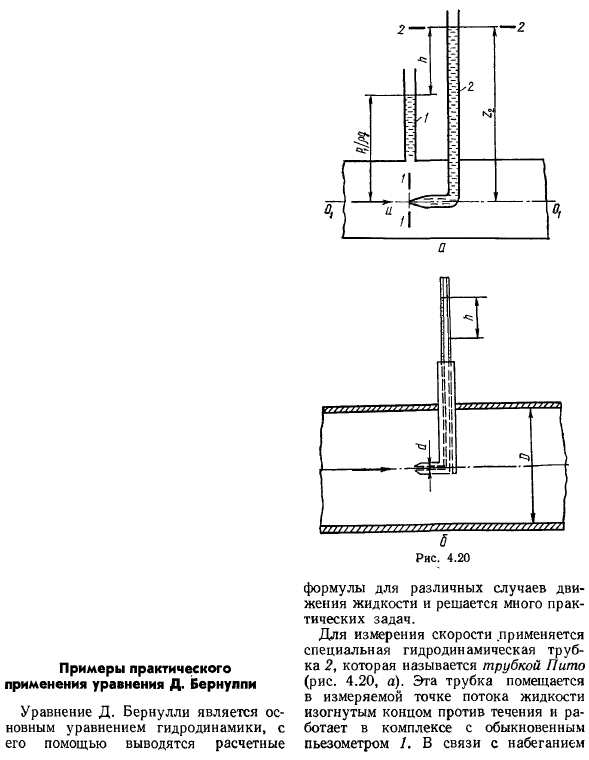
Примеры практического применения уравнения Д. Бернулли. Уравнение д. Бернулли является основным уравнением механики жидкости, вычисленным с его помощью Формула в случае движения жидкости разнообразна и решается множество практических задач. Для измерения скорости используется специальная гидродинамическая трубка 2, называемая трубкой Пито(рис. 4.20, а).Эта трубка размещена в точке измерения потока жидкости и имеет изогнутый конец к потоку и работает совместно с нормальным пьезометром 1. 71.
Трубка Пито 2 пропускает жидкость в отверстие, то есть под действием высокоскоростного давления вода в ней поднимается выше пьезометра 1.Нарисуйте сравнительную плоскость в центре отверстия в изогнутом конце трубки. Рисунок 4.20, а также горизонтальный след плоскости сравнения ОГ-ОГ. Выберите 2 раздела.1-1-перед входом в трубу, и 2-2-на поверхности воды в трубе, D. Я собираюсь написать уравнение Бернулли. Г1. П. С. \ 98. + С128 С±+ 2PR8.
Перепад давления в сужающих устройствах в производственных условиях измеряется обычно дифференциальными ртутными манометрами, а в лабораторных — пьезометрами. Людмила Фирмаль
- Затем-Прандтль сделан из малого диаметра и обтекаемого носа, но даже в этом случае будет наблюдаться турбулентность flow. So, обычно значение скорости, полученное по формуле (4.76), умножается на экспериментально определенный калибровочный коэффициент cp. Заводская труба f = 1… 1.04. Расход воды в трубопроводе обычно определяется с помощью пьезометра или расходомера Вентури (рис. 4.21).Измеритель прокачки Venturi ввод в главную трубу малого диаметра трубы O с ровным входом и outlet.
В узкой части, по сравнению с основной трубой, скорость увеличивается, а давление уменьшается. Сравнительная плоскость Og-Oy выбирается вдоль оси трубы, а участки 1-1 и 2-2 выбираются в предварительно суженной и суженной части. D в этих разделах. Уравнение Бернулли может быть выражено как: Г1 + D. потому что вода не движется через Пито tube. It нет необходимости рассматривать потери энергии уравнения Бернулли. Эта формула описывается в виде основной струйки.
- Это связано с тем, что локальная скорость в точке, где установлена эта формула, измеряется tube. In в этом случае r±-0,0! = И » 2 = 0 (поскольку вода не движется в трубке), измерьте давление на поверхности жидкости в трубке N Rl I » 2 /! = 0, то= r. Как видно из рисунка, r2 =и、 Где k-разность показаний водяного знака в трубке. Следовательно、 И= ущ. (4.76)） Для удобства использования трубка Пито и пьезометр конструктивно встроены в корпус 1 (рис. 4.20, б). Такая трубка называется трубкой пирога РГ. 98. 2 8. 4+ Р а. 98. 4. 28. + ВСН 1-2.
Игнорируйте потери энергии H ^ 1_2, потому что расстояние между секциями невелико, а сужение гладкое. Для горизонтальных труб (rx = r2) используйте коэффициент a = 1. П \ я Г Р2 Р = Р8 + 4 P8 1 2 8 2 8 P \ P * _ 1 C ^ ММ|) 4 П8, П8, 28, 2, 8. Используя уравнение неразрывности (4.30), K,< » 1ио2 я ср т = K2co2,©! =И СО2= -.И затем… УГ _ У2 Т2 -©! ’ 72. Пьезоэлектрический измеренного значения кг = к％ Б. Это отличная игра. Следовательно, = L1-La = 4 «-1 1 Y \ _ х. х. С4. Зная, что U2 Я умею писать. < Е2 H <4 Л4. О4. О, поперечное сечение 0-0： Нужное значение И VI = ио2. −1. 2§к д. О4. (4.77） + B’X ’ 0-G В этом случае r0 = 0, p0 = pa.
Полная энергия жидкости, представляющая собой сумму потенциальной энергии (выраженной величиной давления), и кинетической энергии (выраженной величиной скорости), является, согласно закону сохранения энергии, постоянной, если пренебречь потерями. Людмила Фирмаль
- Фактическое потребление будет несколько меньше теоретического значения (4.77) из-за потерь энергии и может быть выражено в виде зависимости. Р-калибровочный коэффициент, и его значение обычно составляет Р = 0,95… 0.97. D. Используя уравнение Бернулли, расход насоса(?Максимальная высота оси центробежного насоса над уровнем воды в скважине at / g » ac (рис. 4.22) может быть определена Значение очень мало、 Х. Поскольку скорость движения воды в скважине U0 (опускание на поверхность) пренебрежимо мала, ее можно игнорировать без потери точности расчетов. И Ug =V.
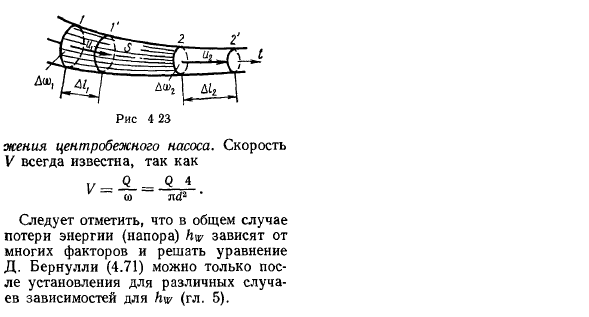
Напишите уравнение Бернулли и отнесите о-к плоскости отсчета Ришор. Секция I вакуумная-1, то есть известная quantity. So … ЛВ.= = ^^Л*. (4.79). Зависимость (4.79) базовая формула для определения высоты местоположения73. Центробежный насос. Скорость V всегда известна. В общем случае потери энергии (давления) k ^зависят от многих факторов, D. Отметим, что уравнение Бернулли(4.71) может быть решено только после установления зависимости km в различных случаях(Глава 5).
Смотрите также:
Возможно эти страницы вам будут полезны:
- Лемма о трех интегралах (по Н. Н. Павловскому).
- Уравнение Д. Бернулли для потока жидкости
- Уравнение количества движения для установившегося потоке.
- Характеристика гидравлических сопротивлений.
