Примеры плоских потенциальных движений жидкости

Примеры плоских потенциальных движений жидкости

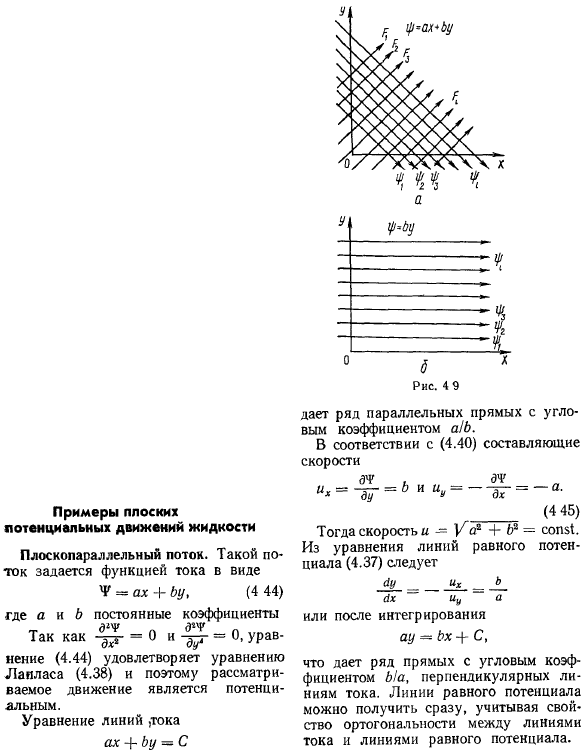
Примеры плоских потенциальных движений жидкости. Плоскопараллельный поток. Такой поток определяется функцией потока в виде рп = ах + ьу,(4 44） Где a и b-посФМтоянные коэффициенты= = 0 и= 0, поэтому уравнение (4.44) удовлетворяет уравнению Лапласа (4.38), поэтому рассматриваемое упражнение является потенциальным. Уравнение линии, ток axbj = C Рю… Рисунок 4 9 ％ ％ Угловой коэффициент a! дайте ряд параллельных линий b. (4.40) в соответствии с компонентом скорости dh. Б и U = = = а. иммуноглобулин. Я буду. dh. (4 45） Тогда скорость u = V a2 + b2 = const1.Из уравнения эквипотенциальной линии (4.37)、 Лу._ _ _ ___ ых Йи в Или после интегрирования ay = bx + C、 Он дает большое количество прямых линий с угловым коэффициентом La, перпендикулярным обтекаемой линии.

Поэтому в рассмотренных при­мерах любая линия тока может быть взята в качестве кон­тура обтекаемой жидкостью поверхности тела. Людмила Фирмаль

• Учитывая ортогональность между линией обтекания и эквипотенциальной линией, эквипотенциальная линия может быть получена немедленно. 58. Рис. 4.9, общем случае плоскость, параллельная рисунок движения, а на рис. 4.9, Б параллельные оси особым случаем движения= = по). Поток вокруг barrier. In в этом случае движение определяется гиперболической функцией С ’= аху (4.46） D как и в предыдущем случае, эта функция удовлетворяет уравнению Лапласа (4.33). _ _ ДХ * + ду * у Поэтому рассматриваемое движение является потенциальным. Уравнение обтекаемости xy = C характеризует семейство равнопроизводных гипербол с осью хны, которая является асимптотой. если вы используете ось x в качестве барьера, асимптота равна x = 0.То есть ось y соответствует центральной линии потока (если C = 0).

Отрицательное значение C помещает линию потока на левой стороне оси Y. На схеме показана общая схема движения при обтекании препятствия. 4.10. Среди составляющих вектора скорости В D. C. Из них= ф = Ну и уй = = ай в Обтекание 4.10 стрелками показано на рисунке. Модуль скорости у = а ух * + У2 = сиг (4.47） Она определяется расстоянием от данной точки до центра, которое прямо пропорционально it. So, скорость осевой линии потока постепенно уменьшается до центра координаты O, а на пределе(r-> 0) скорость также стремится к нулю. Если обе асимптоты принять за стенки, то получится схема обтекания правой angle. By изменяя форму гиперболической функции(4.46), можно получить спектры течения под острым и тупым углом или вокруг пластины.

• Поэтому исследование движения, описанного в функции (4.46), показывает, что жидкость обтекает препятствие, а не сталкивается с ним. Источник и сток на самолете. Источник-это точка, в которой жидкость течет радиально симметрично во всех направлениях(рис. 4.11, а).Слив представляет собой точку, поглощающую жидкость(рис.4.11, б), протекающую симметрично по радиусу. Текущая функция в виде рассматриваемого упражнения является、 ’г» 4-0 §ГС| б-б <4-48> Где f-расход источника или стока (постоянная величина). По аналогии с предыдущим устанавливается соответствие функции (4.48) уравнению Лапласа (4.33). ДТ <2 х вообще〜2л х * + У2〜и* ’ 5. » Это dh2 л(* 2 + У2) 2 ’ d21R, Д2 ^ _ Н dx2 + dn2-и Поэтому рассматриваемое движение является потенциальным.

Если задать различные значения параметра©в диапазоне от 0 до 2 л, то получится линия потока в виде пучка прямых линий, отходящих от центра О. Центральная периферия(рис. 4.11, б) запас. Линии эквипотенциала представляют собой концентрические окружности относительно одного и того же центра. Скорость радиуса в любой точке И затем 1 + 4 = 2л. Yx2 + У2 Х2 + У2 Где r-расстояние от центра О. _0_ 2л / ’ (4.49） Поскольку скорость не бесконечно велика, то зависимость(4.49) нельзя применить непосредственно к области вблизи центра O. дело в том, что они имеют дело не с точками (источниками), а с отверстиями ограниченного size.

Полученный поток получается путем геометрического сложения сторон ячеек, образованных от пересечения обтекаемых линий сложенного потока. Людмила Фирмаль

• Примером стока является водозаборное сооружение в водохранилище, из которого вода вытекает со всех сторон. Добавление потенциального потока. Уравнения Лапласа (4.33) и (4.43) являются линейными дифференциальными уравнениями equations. As известно, что сумма их конкретных решений также является решением этих equations. So, суммируя имеющиеся решения в простейшем потоке различных комбинаций, можно получить более сложные потенциальные потоки различных типов. В качестве примера рассмотрим наложение плоскопараллельных потоков на источник (рис. 4.12, а).

Диагонали каждой ячейки соответствуют направлению вектора скорости и всей линии потока (рис. 4.12, б). Рассмотрим 1 из ячеек(рис. 4.12, б).Теперь у нас есть 2 вектора для любой точки сложного движения. Плоскость параллельна и 2Радиальный ток. Поскольку масштаб потока одинаков, составляющие траектории, по которым частицы жидкости движутся в направлении скорости, должны быть пропорциональны их значениям. A1gA / а че-1 ну ’ Если плотность потока достаточна, то каждую ячейку можно считать параллелограммом. Зададим расстояние между текущей линией, линией и линией соответственно. Хорошее образование.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

1. Уравнение нервзрывности жидкости.
2. Особенности потенциального движения жидкости.
3. Уравнение Д. Бернулли для элементарной струйки установившегося движения жидкости.
4. Лемма о распределении гидродинамического давления в плавноизменяющемся движении.