Оглавление:



Примеры определения предельной нагрузки статическим методом
- Пример определения предельной нагрузки статическим методом. Далее, метод приближенного определения критической нагрузки путем выбора статического возможного состояния, будет называться статическим методом. Этот метод всегда дает приближение от следующего к предельной нагрузке.
Если вы можете перебрать все статически возможные состояния и найти состояние, соответствующее максимальному значению нагрузки, это значение будет точным. Рассмотрим, в качестве примера, непрерывную балку, состоящую из двух равных пролетов, и непрерывную равномерную распределенную нагрузку
q (рис. 1), нагруженную по всей ее длине. 179). Размер этой нагрузки Людмила Фирмаль
необходимо выяснить. По X, покажите реакцию крайней поддержки. Придание X всех возможных значений повторяет все статически возможные состояния луча. Условие, что максимальный изгибающий момент равен 7IT, определяет величину нагрузки q для каждого значения X, а максимальная нагрузка соответствует предельному состоянию. Изгибающий момент в поперечном сечении с координатой x: MX=X —- Максимальное значение крутящего
момента достигается в X1X2, как вы можете легко видеть х=х г—, (компании AFX) Макс=г—. Если мы потребуем, чтобы модуль этого момента не превышал MT、: С другой стороны, максимальные значения крутящего момента могут быть достигнуты на промежуточной опоре х-1. Она равна X I— — — из условия, что абсолютное значение этого момента не превышает AGT, находим: Икс. Я вопрос*<2 Неравенство в безразмерных числах переписывается
- следующим образом: Полученный </ * <2(1-f-X). (a) (b)§ 165J определение предела статической нагрузки 359 Для риса. 244 штриховка указывает области, в которых выполняются неравенства (a)и (b).. Наибольшее значение нагрузки соответствует точке А, где парабола и прямая пересекаются g=2 (L X=L1 в этой точке=2 (1-J-y/^2), соответствующее значение нагрузки=6-{-41^2, достигается максимальное значение крутящего момента пролета). Те, которые были найдены в§ 121 без строгого обоснования. Если система имеет
более высокую статическую неопределенность, если приходится искать максимальное значение предельной нагрузки в зависимости от некоторых параметров, то такой анализ необходим. Восемь. Шесть. Четыре. Два. 1 2 3 4 5 6 Второй пример, который следует рассмотреть здесь, немного меньше. Необходимо нагружать продольную силу P и крутящий момент M
для кругового сечения радиуса G, а также получить отношение распределения напряжений Людмила Фирмаль
и силы к моменту в критическом состоянии. Растягивающая сила вызывает нормальное напряжение o, а крутящий момент вызывает тангенциальное напряжение t, оба из которых являются функцией радиуса Q. Возьмем неизвестную функцию t (e) в качестве искомой функции, o{q)=(oj-ZT (e)’) 1″2. Растягивающее усилие и крутящий момент выражаются через t (e)следующим образом: Г Р=2л у у-ЗТ * Щ йй, Отчет г G=2l в Tg’DQ. Учитывая произвольную функцию t (q), вы получаете различные статически возможные состояния. Чтобы
найти его, нужно найти максимальное условие 360 теории предельного равновесия. XV Сила фиксированного значения момента или наоборот. В ней раскрывается так называемая проблема условных экстремумов. Согласно общим правилам расчета вариаций, мы настраиваем функцию Г Р-ХЛ! =2л^Ф (Х, Т (Г))£?вопрос. О Здесь. Ф(Х, Т (М))=м/с; — ztg по-Хо не. Экстремальные условия значения являются: 0. В этом примере ZT От г __4-Хя=0. 1ag ’ +ztg по Отсюда мы находим T (q)): т/з / з+Ху’ Из условия пластичности определите a (q): a=aT/3^U=. т/ш-н е* Таким образом, распределение напряжений зависело от параметра А, характеризующего соотношение между
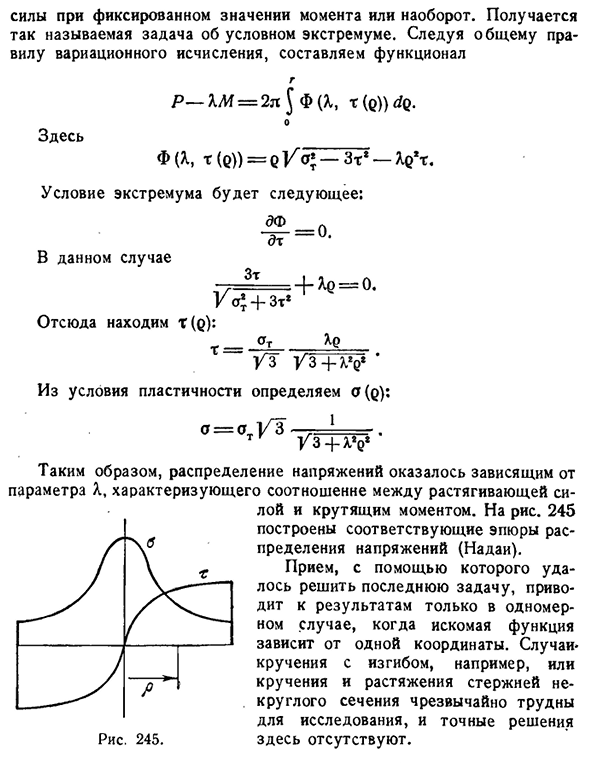
растягивающей силой и крутящим моментом. Для риса. Создайте соответствующий рисунок распределения напряжений 245 (Nadai). Технология, в которой была решена последняя задача, дает результаты только в одном измерении, где искомая функция зависит от одной координаты. Например, в случае скручивания путем изгиба или кручения и натяжения некруглого стержня очень трудно исследовать и точного решения не получается
Смотрите также:
| Истинное и допустимые состояния элемента | Кинематически возможные состояния. |
| Статический метод определения предельной нагрузки | Кинематический метод определения предельной нагрузки |

