Оглавление:




Примеры определения предельной нагрузки кинематическим методом
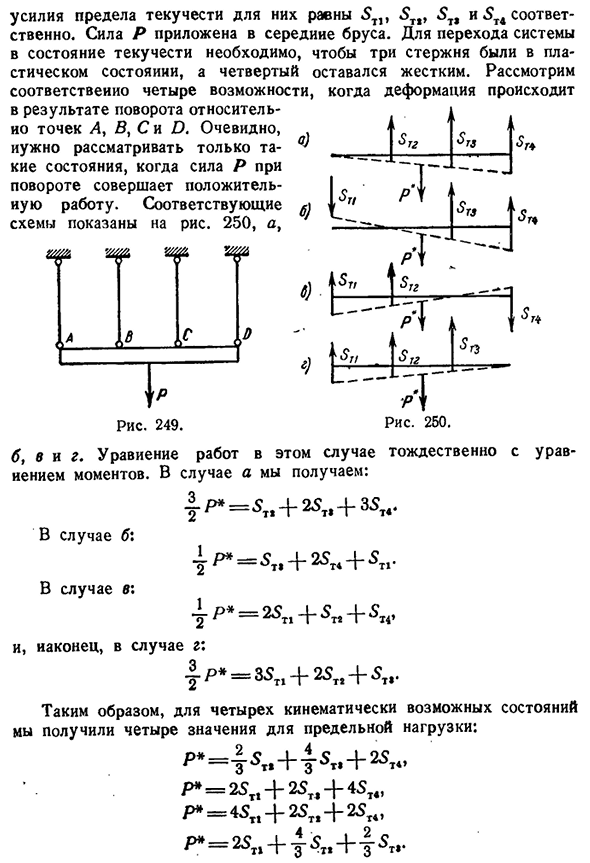
- Приведен пример определения предельной нагрузки кинематическим методом. Кинематический метод гораздо проще и проще в применении, чем статический метод, и поэтому находит гораздо более широкое применение. Рассмотрим два простых примера. А)Ж Е С Т К и й б р У с(Рис. 249) подвешивается в четырех
стержнях в разных поперечных сечениях или в разных материалах; следовательно, конечное равновесие[364 теория гл. Силы их предела текучести составляют 5Т1, 5тт, СТТ и СТ1 соответственно. Сила R приложена к центру луча. Чтобы перевести систему в состояние ликвидности, необходимо, чтобы три стержня
находились в состоянии пластика, а четвертый оставался твердым, поэтому есть Людмила Фирмаль
четыре возможности.、 Рассмотрим, когда происходит деформация смотреть рисунок. Уравнение в этом случае совпадает с уравнением момента. Для A,|P=5T,+25T,+3ST4. Дело в: дело в: 4п=25t1+см+Си4, И, наконец, если g: / P*=3ST1+2STS+5T. Таким образом, для четырех
кинематически возможных состояний получены четыре значения предельной нагрузки: р * =|ст.+4ст,+2st4,Р=2St1+2ст+4St4, P=4ST l -| — 2S T t — / — 2S T4,§ 1 6 8] кинематическое определение предельной нагрузки. Способ 8 6 5 Кинематически возможное состояние, то, что в силу Теперь осталось заменить численное значение предела
- текучести стержня и выбрать наименьшее из четырех значений силы Р. Три других значения силы P, соответствующие статическому, но невозможному, стержню, считающемуся жестким, остаются за пределами предела текучести этого стержня. б) рассмотрим ту же двухпролетную сплошную балку, что и во втором примере, рассчитанном статическим методом в§ 165. Установим регулировку
пластиковых петель в пролете (рис. 251). Если принять во внимание полусферу, то можно увидеть, что работа внешней нагрузки q * равна произведению этой нагрузки на площадь треугольника ADB, то есть угол so-l a g / ’в A4-R равен времени полета? * =АФИ(4-2П). » Заметим, что, уменьшая p=a на A и вводя безразмерную нагрузку таким же образом, как§ 165, вы получаете: ’•=4t+^1 ) — Условие минимальной нагрузки приводит к следующему уравнению 5′ 4 — 2 5 — 1 = 0. И так оно и есть. / = / 2-1 (Второй маршрут не имеет смысла).
Правильное отклонение нагрузки 7=6 4 — 4 / 2 Соответствует значению, Людмила Фирмаль
найденному статическим методом. Для решения этой задачи в § 121, по существу, применялись также кинематические методы. Без строгого обоснования кинематический метод использовался в течение длительного времени и довольно широко в сопротивлении материала. Предложен ряд приближенных методов расчета на основе ИА.366 теория предельного равновесия[гл. XV .Гипотеза определенного характера обосновывается теоремой, доказанной в предыдущем пункте. Поэтому, если внимательно посмотреть
главу IV, которая посвящена в первую очередь условным расчетам, то эти условные расчеты основаны на предположениях определенных кинематических планов разрушения, и введенный в расчеты запас прочности точно необходим, так как неизвестно, на сколько истинное значение нагрузки превышает верхнюю оценку. Если имеется приближенное решение, полученное как статическим,
так и кинематическим методами для одной и той же задачи, то положение становится более ясным и получается двунаправленная оценка. Иногда им удается собраться вместе так, что поиск точного решения теряет свой смысл. Однако более трудно найти статическое решение, и есть точные оценки для некоторых проблем.
Смотрите также:
| Кинематически возможные состояния. | Предельное равновесие пластинок |
| Кинематический метод определения предельной нагрузки | Колебания систем с конечным числом степеней свободы |

