Примеры линейных моделей

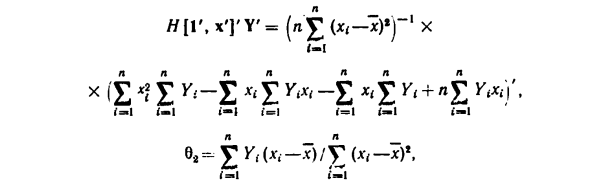
Примеры линейных моделей

• Пример 1. Пусть У = (Уи У2 Йн) независимая выборка из N (\ i, а2) с неизвестными ц и а. Представим наблюдения в форме эй, я = л, …, п, а) где е, -— независимые Н @, 1) -распределенные ел. в. Вводя л-мер- определенные видимые строки 1 = A, 1, …. 1), е = (е!, …, е „), запишем A) в векторной форме ? = ц-1 + ов. б) Поставим задачу отыскания линейной несмещенной оценки пара- 69 пусть b = (fc, Ü „) -чис- числовой вектор, такой, что статистика в) несмещенно оценивает ц (знак транспонирования ‘означает пере- переход к вектору-столбцу): Отсюда следует, что вектор должен удовлетворять условию Дисперсия оценки C) равны D (bY ‘) — &, Ч> У, + … + B

Хорошо известно, что таким вектором является Ъ = п ~ 11, т. Т. На- наилучшая линейная несмещенная оценка выборочным средним A = -II = я D) t = -i Подчеркнем следующее важное обстоятельство: при решении задачи отыскания наилучшей линейной несмещенной оценки были используются только свойства моментов ел. Ме, = 0, / = 1, …, п, = l, …. п] = /, E) где / -единичная матрица. чтобы рассуждения, приводящие к оценке D), сохраняют свою силу и когда есть. в. е., я = l, имеют доступное совместное рас- доля вероятностей. Пример 2 [6]. л = 15 измерений влажности некоторого материала, проведенных

Таким образом, оценка C) будет наилучшей, если вектор b имеет сумма координат равна 1. Людмила Фирмаль

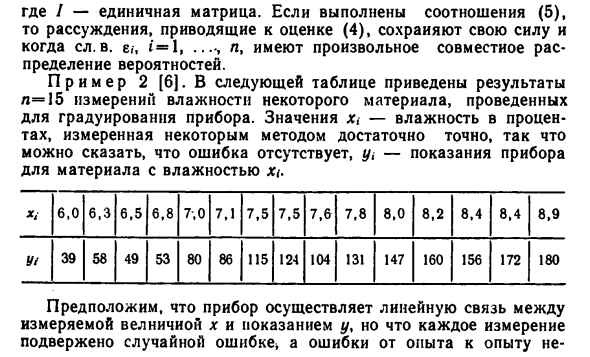
Значения х, -влажность в процентах процентах, измеренным можно сказать, что ошибка отсутствует, «/, — показания прибора ДЛЯ У / материала 6,0 39 6,3 58 6,5 49 с влажностью х 6, 8 53 7,0 80 7,1 86 7,5 115 «• 7,5 124 7,6 104 7, 8 131 8,0 147 8,2 160 8,4 156 8,4 172 8, 9 180 Предположим, что прибор представляет собой линейную связь между измеряемой велничиой подвержены случайной ошибке 70 коррелированы и имеют одинаковые дисперсии о2. описание рассматриваемого опыта можно предложить модель или Y = 8, l + 82x + ae, вектор е подчиняется условию E), а, 8i и 02-неизвестно неизвестные параметры, х = (хи хг х „). Пусть а = (аь а2) -произ- возможный числовой вектор. несмещенно оценивающую линейную комбинацию неизвестных параметров 8 0 е ‘

В састных случаях а = А, 0) и а = @, 1) получим- исходящие оценки для 0 | и 62. По условию несмещенности л л мы =? ь, му, =? ь (@ t + е, *,) = я = я я = -i л л каковы бы ии были 0 | и 02. . =. 1.-Я или (ЬГ, bx ‘) = b [l’, х ‘] = („о,). F) Дисперсия оценки л л DbY ‘=? IfoYi =? Ь? «« = А * || b || J. G) я = -i. = -1 Таким образом, среди всех векторов, удовлетворяющих F), надо Заметим, что если наименьшую длину. Ь-любой вектор, удовлетворяющий F), то его проекция на линейное подпространство V, порожденное векторми 1, х, очэ иидно, также удовлетворяет F), длина проекции ие превосхо- превосходит длинная волна. длины, удовлетворяющего F), мы ничего не потеряем, если которые лежат в подпространстве подпространстве V: Ь = с, 1 + с2х.

• Подставляя (8) в условие несмещенности F), получаем С | 1Г + с2хГ = а |, (9) Определитель системы (9) равен л л 2 я = -l я-л 1 = 1 и если в этом случае существует единственный вектор b в форме (8), дающий несмещенную оцен- оценка, следовательно, соответствующая оценка минимальную дисперсию. Вычисляем матрицу, расположение к матрице системы (9): X — Ух п так что решение системы (9) предегавимо в виде (Си С2) = (аи а2) Н.

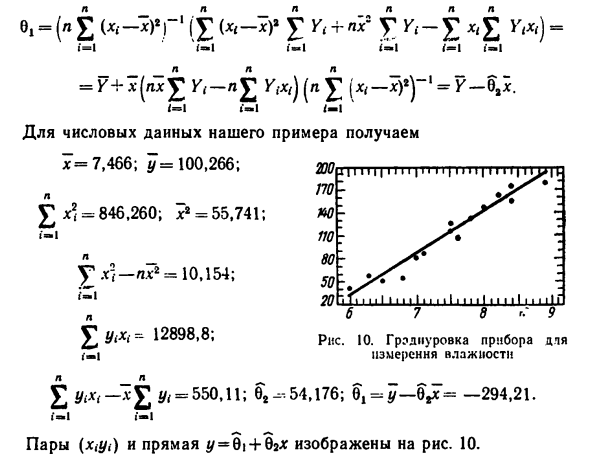
Находим оценки параметров 6i, 62 (см. (8)): ei-bY’-fo, сг) [\ ‘, х’] ‘Y’ = (fll, at) H [V, x ‘] Y’ = A, 0) H [V, x ‘]’ Y ‘. ‘, x’,] Y ‘. Проведя элементарные выкладки, найдем окончательные формулы для 6 ,, §2: х 1 = 1 л л л л л л 1 = 1 (-1 1-1 1 = 1 1 = 1 * = -1 л л Yt + NT 8 = 1 = 1 72 .— * J.г ‘(? (* — (= 1 1 = 1 ) \ Z * \ ») 2 ¦ (-1 Для числовых данных нашего примера получите х = 7,466; # = 100,266; л * t = 846 260; х2 = 55 741; • «= ¦1 / (/ Если по 50 ? П я 111111 «Я фт 1111 1 1 1 1 • 1 111 III 11111 11 I 1 1 1 1 у • III II ¦ ii я Illl ^: я болен * х} —пхг = 10 154; = 12898,8; = 550,11; 62-54,176; вх = ^ -6 ^ = -294,21. 8 Рис. 10.

Гроднуровка прибора для измерения влажности Пары (Xitfi) и прямая (/ = 6 | + 6гХ изображены на рис. 10. Людмила Фирмаль

Смотрите также:

Предмет статистики

Доверительные оценки для н и о2, когда один из параметров известен	Линейная статистическая модель
Сравнение дисперсии в двух выборках	Наилучшие оценки в случае матрицы неполного ранга