Оглавление:








Примеры и определения
- Примеры и определения Мы уже обсуждали понятие переменных, независимых переменных и функций, но рассматривался только самый простой случай. Вот несколько примеров переменных и констант: 1. Наиболее распространенной переменной является время. 2. Переменная — дневная температура. 3. Отношение окружности к диаметру постоянное — это число i. 4. Гравитационное ускорение является постоянным, но это верно только при соблюдении определенных физических условий. 5. Температура кипения химически чистой воды постоянна и равна 100 ° С, но это верно при нормальном атмосферном давлении.
Поэтому наблюдайте переменные, которые являются константами и условными константами. Определение Две переменные называются функционально зависимыми, когда их значения соответствуют одному или нескольким другим конкретным значениям. Если каждому значению независимой переменной соответствует одно значение функции, функция вызывается явно, в противном случае она называется многозначной.
Первое значение называется независимой переменной, а второе значение — зависимой переменной или функцией. Людмила Фирмаль
Линейные функции, все тригонометрические функции, экспоненциальные функции и логарифмические функции являются уникальными.Неявные функции, которые определяют круг, эллипс или гиперболу, являются двоичными или многозначными. Вот еще пример функции: Если вы используете электрическую цепь, которая включает в себя источник постоянного напряжения и резистор, вы можете получить разные токи, изменив значение сопротивления. В этом примере напряжение V является постоянным, а сопротивление R и ток I являются переменными. Отношения между ними устанавливаются законом Ома.
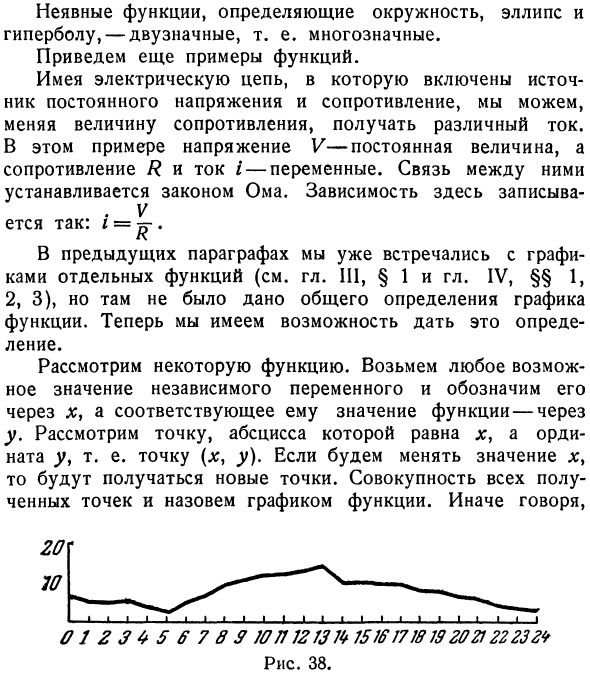
Зависимость здесь , V выглядит так: г • В предыдущем абзаце мы уже встречали графики отдельных функций (см. Главы 1, 1 и 4, главы 1, 2 и 3), но общего определения графиков функций не существует. Это было Теперь есть возможность дать это определение. Давайте рассмотрим некоторые особенности. Возьмите возможное значение независимой переменной, укажите его с помощью x и укажите соответствующее значение функции с помощью y. Рассмотрим точку, абсцисса которой равна x>, и ординату y, т.е. точку (i, y). Изменение значения х даст новую точку. Вся полученная точка называется графом функций. Другими словами, 01 2 3 4 5 G 7 8 3 UI11213 K15 W17 Iff 19202122232 <г Рисунок 38.
- График функции — это геометрическое положение точки, абсцисса которой равна значению независимой переменной, а ордината — соответствующее значение функции. Как видите, ранее рассмотренные графики соответствуют этому определению. Рисунок 38 представляет собой график суточных изменений температуры. Вы можете использовать этот график, чтобы найти температуру в определенном месте за прошедший день.
Так, например, в 8 утра (по горизонтальной оси 8) Температура составляет 10 градусов Цельсия (вертикальная длина перпендикуляра от найденной точки до оси абсцисс составляет 10 единиц в приемлемом масштабе). Следовательно, график, показанный на рисунке 38, устанавливает соответствие между каждым моментом и числовым значением, указывающим температуру в этот момент. Замечания.
Функция — это не только зависимая переменная, но также закон или метод, который устанавливает соответствие между зависимой переменной и независимой переменной. Например, если задана функция y = x ‘+ yx, можно сказать, что задана функция xx + yx. Есть несколько способов определить функцию. В большинстве случаев функции определяются уравнениями, таблицами или графиками. Например, линейная функция задается уравнением. Возможность изменения температуры в течение дня обычно устанавливается по расписанию.
Зависимость угла прицеливания от расстояния приведена в таблице. Людмила Фирмаль
Так же, как символы вводятся в алгебре для обозначения чисел, общие функции вводят следующие обозначения: Если y — функция, ax — независимая переменная. Y = f (x). Где / указывает набор и порядок математических действий (сложение, вычитание, умножение, деление, мощность, мощность, логарифмический поиск, тригонометрический поиск и т. Д.). Для того, что необходимо для выполнения перечисленных действий, поставьте / введите рядом с скобками, которые они описывают. Обозначение y = f (x) читается следующим образом: у имеет функцию х.
Пример 1. f (x) = Vx *, где / равно 1), возведенное в третью степень. 2) Добавить один. 3) Извлечь квадратный корень. Пример 2. y = zf (x) = 2s \ nx. Где / означает следующее: 1) Найти значение знака. 2) Умножить на 2. Пример 3. Y = f (x) = x * + 4×2 +5. Где / означает: 2) Повышение до второй степени. 3) Умножьте результат, полученный в предыдущем абзаце, на 4. 4) Добавлены цифры, полученные в пунктах 1 и 3. 5) Добавьте 5 к тому, что вы получили раньше.
Пример 4. Функция f (x) определяется следующим образом: Если x <0, то f (x) = 0, если O ^ x ^ l, если f (x) = 1; *> 1, то / (q 🙂 = 0. В этом примере функция / (x) не показывает математическое поведение и операцию, представленную через jc, но ее значение все еще можно указать для любого x. Например, x = −3. В этом случае f (−3) = 0, поскольку выполняется неравенство −3 -1, поэтому /(11,5) = 0 Эти типы функций встречаются не только в математических учебниках, но они часто встречаются в современной физике и технике. Рассмотрим схему, показанную на рисунке. 39. Где B — источник постоянной электродвижущей силы (например, аккумулятор), B-переключатель, A-амперметр, R-сопротивление. Рисунок 40. Рисунок 39.
Когда переключатель разомкнут, ток не протекает по цепи, и амперметр показывает ноль. Когда переключатель замкнут, на цепи отображается постоянный ток, а его значение отображается на амперметре. Стрелка амперметра не всегда двигается, пока выключатель не выключен. Если вы нанесете время на горизонтальной оси, а текущее / на другой оси, этот зависимый от функции график будет выглядеть как рисунок. 40. На этом рисунке показан момент, когда ток включен, и момент, когда tt выключен.
Существует бесконечное множество функций, поэтому невозможно или необходимо дать каждому конкретное имя. Тем не менее, некоторые очень общие функции названы. Вот некоторые из них: Линейный, квадратичный, тригонометрический, логарифмический, экспоненциальный, степенной многочлен (или просто многочлен) вида y * = aQxn + + agnn-1 + … + an.
Смотрите также:
| Логарифмическая функция | Область существования функции |
| Некоторые простые неявные функции | Функция от функции, или сложная функция |

