Оглавление:




Примеры
- Образцы. П р и М Е Р5. Изготавливается цепь=4Т, которая помогает поднять груз Р(рис. 12) сделанный из круглой стали с прочностью на растяжение%= = 37 кг’млр. Коэффициент запаса прочности k=6. Найти необходимый диаметр звена dy для ограничения учета растягивающей силы на ветви цепи. Закругленная часть имеет напряжение из-за изгиба. Поскольку сила Р действует на ось звена, она равномерно распределяется между сторонами. Условие,
определяющее регион. Каждая ветвь ссылки имеет следующий формат П Допустимое напряжение[C] равно[a]= — ^ = ™-617 кг/СМ1. Итак, площадь поперечного сечения ветвей выглядит так П Двухтысячный. Шестьдесят семь. =3. 24cm2, И диаметр штанги звена d=y R^=j/r-4’3^2 4-=2.03 в» 2.1 cm. П р и М Е Р6. Кронштейн ABSU, состоящий из деревянного бруса as и железного бруса AB,
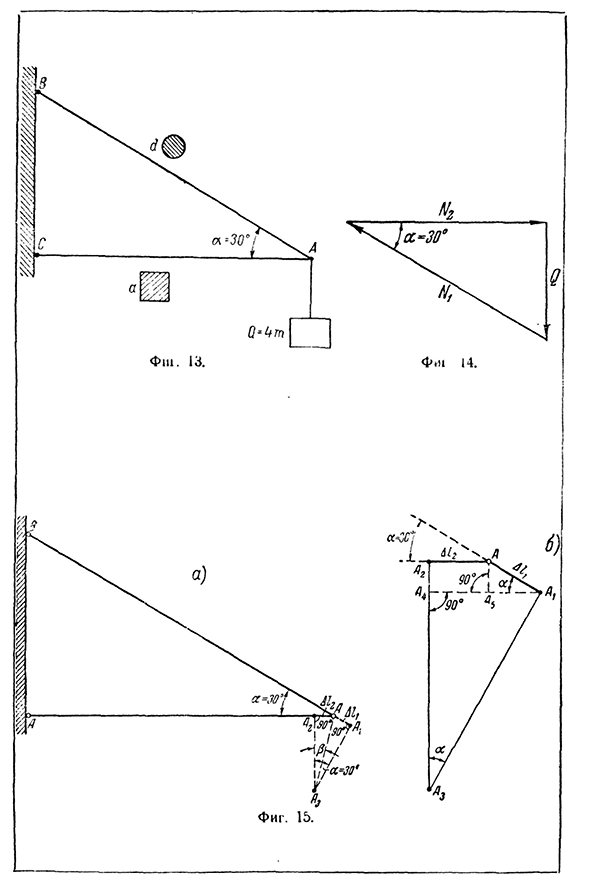
имеет нагрузку Q—4t, подвешенную в точке A(рис. 13). Поперечное сечение Людмила Фирмаль
стержня AB круглое, а стержень AC квадратный. Диаметр стержня AB d и стороны квадрата a (если допустимое напряжение стержня AC\Wood[c_[=25 кг) см2, а также допустимое напряжение сжатия, [j -=] см2, [C+[==900 кг>см2 (т. е. -)] стали. Ni и N2 в стержнях AB и AC находятся из равновесного состояния шарнира A, известные силы Q и неизвестные силы LGH и N уравновешиваются этими силами (14),
получаем M=y o g2 0=8GM=; TV 6930K l-25=277 см. Диаметр стержня равен =3. 34cm3. 4см; Сторона квадрата равна B=/? , = /2 7 7 » 1 6 ,6 см^1 7см;оба значения в СМ на весь мм к стальной полюс для древесины…Взято, с округлением. Чтобы определить движение / точку A, увеличьте или уменьшите новую длину bai и SL2 с bis^A A i и D/8=IL8 без изменения направления стержня(рис. 15, В нет. Чтобы найти новое положение точки A, держите деформированные стержни
- вместе и вращайте их вокруг точки B и точки A. тогда горизонтальное перемещение точки A будет выглядеть следующим образом / 8= = AAS=AZg, и вертикальный (рис. 15, б) f=A9aya=AYAA<4~A, At. Резать А$A4ss а б л / т грехе л, Но a4a,=а,, J. Но ai4 предусмотрены=ОП с Д-D5D4=Д/J в cos4-Д / 8,так что Аль-4al т=, (Да/т и Кос 4. — Да z /%1M COS8 4-D / 8cos Восемь. ) 5 — — ——— ‘ СЧ грех Тогда L/= ‘АА Иал, 4И-Л Л=Да/>1С•я н А4І- — — М—1—С-О-С-8—а-Г4 -] — — — — Д—/8— С-О — С — — — а — =д/л>ж-ж/8COS а Грех есть грех а Деформация стержня определяется по формуле да/, _ ^ » _ 6 930- 100 1L_ * — JQS. 17″ — 2L-1°C -«, N t/t8 0 0 0 0 0 0 0 0.Два. 1=£л Таким образом, горизонтальные вертикальные — —————————- = 5,07. 10-2 см 2-10* • 移動点aはL=に等しい0.24.BH, полное смещение sin a A A t равно 0,507 4- 0,24 1 4 2 из 1.43 мм, 0.5 /=G I+I=G1.
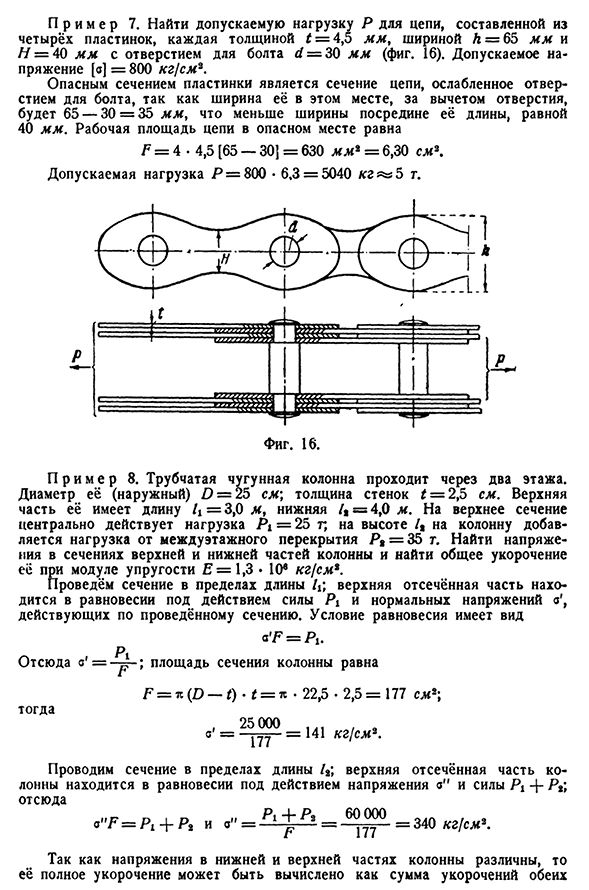
43″+0.24 «» 1.45 MM44 растягивающие и сжимающие напряжения и деформации[CHAP. II П р и М Е Р7. Найти допустимую нагрузку Р цепи при каждой толщине l=4,5 мм, ширине L=65 мм, H=40 мм, отверстии под болт d=30 мм. 16). Допускаемое напряжение [о]=800кг! см* Опасная часть пластины-это часть цепи, ослабленная отверстием для болта, ширина в этом отношении минус отверстие составляет 65-30=35 мм, а ширина в середине его длины-40 см.= 4 • 4,5 [65 — 30] = 630 мм * =6,30 см. Допустимая нагрузка R=800•6,3=5040 кг^5Т. П р и М Е Р8. Трубчатые чугунные колонны проходят наверх. Его диаметр (снаружи)D=25 см -, толщина стенки d=2,5 см. Его верхняя часть имеет длину Zi=3,0 м, нижняя Zg=4,0 м, а верхняя часть представляет собой нагрузку a=25 г, действующую на середину, а высота Zg на колонну прикладывается к нагрузке от пола P g=35
т. Верхняя отрезная часть находится в равновесии под действием силы Pi и действует на ту часть, где нарисовано нормальное Людмила Фирмаль
напряжение a’. Равновесное состояние принимает вид Следовательно, ’ = Πp a’R=R1. ;Площадь поперечного сечения колонны равна Затем Ф=К(Г -£). £ = K• 22,5 • 2,5 = 1 7 7 Смотреть-, Двадцать пять тысяч Сто семьдесят семь. =141кг}см. Нарисуйте участок длиной Z2; верхняя отрезная часть колонны находится в равновесии под действием напряжения o «и силы + Pt, и поэтому(P,+P) 3) / 3 60 000 • 400 _ , П Л»» ~ ——-ее.———— 1,3’.Т0 ««177~» °4 М Л1′ Полное сокращение может быть следующим D / =D / 14-D’. = = 0,33 + 1,04 = 1,37 ««1,4 хм. ФВ Это сокращение может быть рассчитано по-разному. Сила P2 и реакция, вызванная этой силой, получаются отдельно как сумма укорочений, вызванных каждой силой, и равны 7_Pl (A+M, PgZs EF). (П4-П2)12. П укроп » эф эф* Как и ожидалось, уже пришли к формуле, полученной ранее.
Смотрите также:
| Деформации при растяжении и сжатии. Закон Гука | Диаграмма растяжения. Механические характеристики материала. |
| Коэффициент поперечной деформации | Диаграмма напряжений |

