Оглавление:











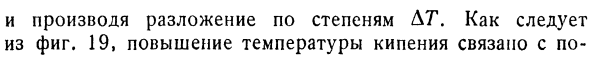






Примеры
- Осмотическое давление.Разделение различных областей концентрации в растворе с помощью полупроницаемой мембраны, например, где растворитель проходит свободно, но растворенное вещество не проходит, приводит к частичному равновесию в системе. Это частичное равновесие заключается в том, что химический потенциал растворителя одинаков с обеих сторон мембраны, в то время как химический потенциал растворенного вещества различен и не может быть уравнен из-за его presence.In в классических лекционных экспериментах, показывающих осмотическое давление, водный раствор соли 1 отделяют от чистой воды 2 бычьим пузырем (рис. 18).Вода проникает в полость 1 и поднимает уровень манометрического капилляра до тех пор, пока гидростатическое давление не уравновесит диффузию чистой воды в раствор. Решение г. Вода. F и d. 18.
Осмотическое давление.)%( год’-’ / 、* 1, р и-// в Величина осмотического давления может составлять несколько атмосфер, и мембране необходимо выдержать его, когда она достигнет равновесия.Осмотическое давление имеет важное значение для живых организмов, и исторически концепция осмотического давления сыграла огромную роль в развитии термодинамики.По этим причинам в качестве примера данной главы мы выбрали термодинамическую теорию осмотического давления, предложенную Ван-Хоффом (1903). Сделать молярную долю воды в растворе равной х. химический потенциал воды в объемах 1 и 2 (см. Рисунок 18) должен быть одинаковым.Сделать давление с обеих сторон мембраны равным Px и H2, respectively.In в случае воды эти давления не могут быть равны = х),(6.110)
Это избыточное гидростатическое давление называется осмотическим давлением. Людмила Фирмаль
Это происходит потому, что противоположная концентрация мембраны отличается.Вы можете написать больше РГ. \ я(Р2)= \ я(ЛП)+ \ вдп. (6.111) Я… Если игнорировать малую степень сжатия для воды (- d \ nV / dP-10 атм-1)、 / я (Р2.х)= \ х (ПВ х)+ в (П2-ПЗ). (6.112) В этой формуле P2-Px = n-осмотическое давление, а v = vQ — d \ x (dP = du’DP dN0-парциальный молекулярный объем воды. Когда Формула (6.105)применяется к растворителю в разбавленном растворе и Формула (6.110) замещается (6.112、 Ли—кт 1П х0. (6.113) Логично заменить логарифм первым членом разложения ряда Тейлора, так как он ограничен рассмотрением дилатационного решения 1p * 0 = 1p(1 =-•••»(6.114) 5. Здесь, как уже говорилось, индекс s соответствует растворенному substance.In в этом приближении вы в конечном итоге получите формулу Ван Гога осмотического давления я =(6-115) Где n-количество молей растворенных веществ в объеме V. Том V здесь делает вывод, что это Nv0 — \ — minor term.In в случае разбавления раствора, различать удельный объем v°от частичного объема v и растворителя не имеет четкого смысла.Однако, учитывая разницу между v и v°, результаты согласуются с экспериментами с гораздо более широким диапазоном concentrations.
So я написал V, а не V (V), а не V (V). 5-й случай с высокой степенью dilution.So, осмотическое давление равно давлению Р-моля идеального моля, который содержится в определенном объеме.Согласно традиции, это интерпретируется как избыточное давление из-за того, что на одну сторону мембраны воздействуют молекулы растворенного вещества.Это выражение облегчает запоминание выражения (6.115), но его не следует толковать буквально.Если эта формула верна, то она обязательно должна применяться к идеальному решению.
Однако при выводе использовалось приближение (6.114), поэтому даже для идеальной смеси формула Wapt-G’off может быть применена только для расширенного разбавления.Для идеального решения формула (6.113) может быть применена в любом concentration.It очевидно, что невозможно использовать такую простую газокинетическую интерпретацию, поскольку концентрация осмотического давления, полученная в этом случае, содержится под логарифмическим знаком. В заключение рассмотрим несколько численных примеров. Водный раствор, содержащий 1000 г сахарного тростника на 1430 г воды, оказывает осмотическое давление 30 фунтов на квадратный дюйм при 30°C. молекулярная масса сахарного тростника c12h22op составляет 342, поэтому количество молей на 1000 г воды составляет
1кв п-342 — = 4.18. Принимая V-1 ООО см3(объем чистой воды 1000 г), формула Вант-Хоффа имеет вид I == 4L8 * 76 «?356-981 ′ 1Ж * 303 = 104 атм■ Таким образом, мы видим, что теория, разработанная для предельного случая бесконечного разрежения, дает в этом случае относительно низкую точность.Однако эта теория предполагает, что частичный молярный объем воды Молярный объем будет близок к 17Н. о-фактически, если использовать дробный объем вместо определенного объема воды в рассматриваемом примере, то формула Ванта-Хоффа очень хорошо совпадает с l-148,5 атм. В экспериментальном значении мы определяем vu 0 = — dV / dN, но не будем касаться этого вопроса, так как необходимо знать плотность раствора сахарозы в определенном диапазоне концентраций. 2.Давление пара разбавленного solution.In связь с уравнением Клапейрона, мы рассмотрели давление пара чистого substance.It предполагается, что растворитель находится в равновесии с паром при определенной температуре.Когда вещество в жидкой фазе растворяется, давление пара должно изменяться для поддержания равновесия.
Пусть давление пара чистого растворителя равно I, а давление пара над раствором-P-f-DJ.Значения, связанные с газовой фазой, помечены strokes.In новое равновесное состояние、 | я = / я ’(6.116) Каждый элемент.Мы можем в основном рассматривать растворитель, учитывать концентрацию растворенных веществ, так что изменение давления пара невелико, поэтому мы можем написать разложение ^ (- ДЯ, XV …)=!\ Я°(п. т) — т х-\ — vЯЯ+ —- Если мы присвоим это выражение (6.116), то Дя =—в-Дж (6.117) V-V x x (Начиная с Dp, если n = = 1, 0=).Далее, 1) Если пар ведет себя почти так же, как идеальный газ (v ’^ kT / Py, 2) парциальный молекулярный объем конденсированной фазы пренебрежимо мал (v <^ iv’), 3) растворенное вещество нелетучее x’s = 0), то объем конденсированной фазы пренебрежимо мал. Снова разверните логарифм, как в(6.114), и найдите формулу относительного декремента*) !)
Например, если растворенное вещество является очень Летучей жидкостью, то естественно, вместо падения может произойти повышение давления пара.Случай также может быть описан в рамках простой теории, если концентрация достаточно мала.Тогда есть знак DR / I 2 с. Положительный, если концентрация пары выше, чем концентрация жидкости. Давление пара: =(6-118) Давно известно, что давление паров раствора ниже, чем у чистого растворителя, и это снижение давления примерно пропорционально концентрации растворенного вещества.
Формула, выражающая закон, предложенный Раулем (1888)и названный в его честь(6.118), является первой простой проверкой применимости приближения, точнее, формулы (6.108), которая лежит в основе теории разбавленных растворов. 3.Точка кипения rises.As результат того же эффекта приводит к снижению П. С. Растворители 1 атм / / раствор > АР 4Т. F и G. При давлении пара температура кипения раствора увеличивается по сравнению с температурой кипения чистого растворителя. 1-е повышение температуры кипения можно найти обычным способом, который выравнивает химический потенциал растворителя в жидкости и паре (х (1 атм, Т + Д7 \ х / т…) = | d /(1 атм, T — {- D7 \ x’R (6.119)
Выполните расширение с силой ЛТ. 2 19, подъем в Точке кипения Более низкий коэффициент давления пара _ разность потенциалов < 6L20> Из закона Рауля можно сделать следующие выводы: давление паров чистого растворителя и давление паров раствора строго пропорциональны друг другу.Подобный этому Р = РО + др = РО(1 = хр° Следовательно、 ДП-0. — Джей-Джей — диджей(1 + XJ в срок заказа (6.121) В точке кривой давления пара чистого растворителя производная определяется уравнением Клапейрона ДП Ми (6.122) ДТ-г ДК ’ Следовательно、 ГЛК ЛВ. Т ДК РТ. л: ’ = = = ~ ~ d77 ~~ я ^ АУЯ я == d77 ДК—х Или с тем же приближением, что и раньше、 ГД РТ
- Для нормальной жидкости энтропия кипения пара равна −20 кал / моль.Привет! {Правила трутя).Поэтому относительное увеличение температуры кипения такой жидкости определяется приближенной формулой — ^L-o. iJ*,, (6L24) То есть 10% относительного снижения давления пара. Было также подтверждено, что температура замерзания раствора была ниже, чем у чистых растворителей.Формула для снижения 4.Solubility.In в предыдущем примере все определялось химическим потенциалом растворителя, но в случае разбавленного раствора он совпадает с химическим потенциалом растворителя идеальной смеси.Для растворенных веществ、 =(6.125)
Если температура замерзания соответствует (6.123), то такие же соображения должны быть приняты и в отношении жидко-твердой фазы. Людмила Фирмаль
Как упоминалось ранее, важным отличием является то, что постоянный член^(H, T)не совпадает с членом в Формуле идеала mixture.In в этом случае потенциал зависит от свойств как растворенного вещества, так и растворителя, которые должны быть указаны при необходимости.Потенциал f связан с растворимостью.Установить эту связь. Рассмотрим чистое твердое тело, находящееся в равновесии с насыщенным раствором.Растворимость получают путем приравнивания твердого химического потенциала[x°к химическому потенциалу (6.125) этого вещества в растворе. х =(6.126)
Из Формулы (6.125) можно получить простую формулу распределения x далее.XG растворенных веществ между 2 смешивающимися жидкостями, одна заливается сверху other.In случай равновесия, очевидно Ил. = ) / ЛГ(6.127) Правая часть этого соотношения зависит только от температуры и давления, поэтому отношение молярной доли растворенного вещества обоих растворителей должно быть постоянным при любой концентрации (закон распределения Нернста). кроме того, из Формулы(6.125) видно, что такие уравнения справедливы независимо для каждого растворенного вещества.
Однако все вышесказанное справедливо лишь в крайних случаях запущенных отказов. В практических растворах, поскольку растворенные вещества взаимодействуют друг с другом, особенно с растворимостью.Таким образом, можно найти отношения между членами следующего порядка развертывания (см.§ 9) класс защиты = ^ / skxk(6.128) к. Мы будем использовать экспериментально наблюдаемые величины, но не будем об этом говорить. В качестве проверки для метода распределения, мы будем принимать во внимание данные йода, растворенного в воде и 4 хлористых углей.Если концентрация йода 1>в четыреххлористом углероде составляет 6,996 г / л, то концентрация водной фазы составляет 0,0818 г / л, а коэффициент распределения обеих фаз равен 0,0818 / 6,996 = 0,0117.
Если концентрация йода в четыреххлористом углероде равна 25,61 г / л, то концентрация в воде равна 0,2913 г/л. То есть коэффициент распределения равен 0.0114.At в умеренных концентрациях коэффициент распределения йода между двумя фазами находится в пределах этого диапазона достаточно близких значений.Поэтому в этом случае коэффициент распределения растворенного вещества между 2 растворителями остается практически постоянным даже при высоких концентрациях.
Смотрите также:
| Неидеальные растворы | Электролиты |
| Разбавленные растворы | Химическое равновесие.Координация реакции |

