Оглавление:





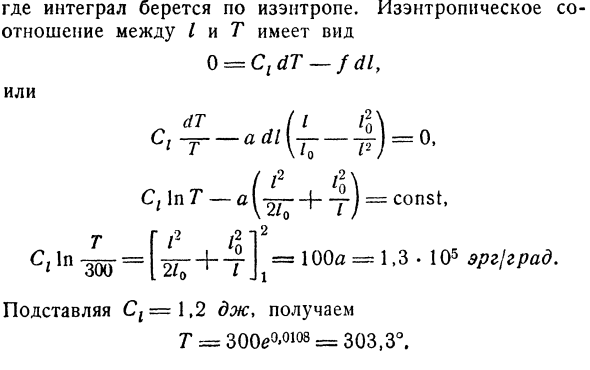

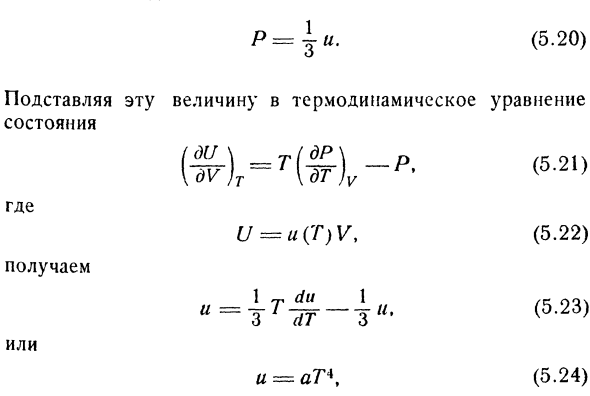










Примеры
- Соотношения Максвелла.Во-первых, мы преобразуем производные (dSjdV) T и (dSjdP) Р. Согласно (5.11)、 ДФ (ДГ \ ДТ)г-ДТ С= Так… (OS \ _ d2F (OS \ _ dU dVJr-OT0V и \ dR) r-dR OT Из уравнения(5.11) (* Л \ = Р(Ш)= Г \ дв) \ Т ОП ^ ) Откуда? Формула (5.16) называется отношением Максвелла.Они оказались полезными в ряде случаев (например, см. Главу 5,§ 3, пункт 3).
- 2.Термодинамическое уравнение состояния.Здесь мы рассмотрим производные (dU, dV) T и (dN / dR) m, которые фигурируют в описаниях экспериментов Гей-Люссака и Джоуля-Томсона(см. Главу 2, Главу 7 и Главу 2).Мы уже работаем над превращением первого из них в парня. 2,§ 7, пункт 1 Но от более простого способа, а именно отношения 1518.) Получить уравнение (дю ДТ)V л (5.19)) Это называется термодинамическим состоянием equation.As увиденный в chapt. 2,§ 7, параграф 2.Левая часть этих уравнений в частных производных определяет изменение температуры газа при адиабатическом расширении.Приравнивание левой части уравнения(5.19) к пуле дает закон идеального газа Бойля-Марио-Гая-Руссака (см. задачу»с»в главах 2, 7 и 2).) — Спросил я.
Уравнение состояния резиновой ленты имеет вид Где / — напряжение, a = 1.3.103 dyn!Град, I-длина,/ 0 = 1 м. a. указывает, что внутренняя энергия зависит только от температуры. а. полоса подвергается обратимому изотермическому растяжению при температуре 3°С, длина изменяется от 1 до 2 м. Найти работу, выполненную на полосе и количество поглощенного тепла. c. если полоса растягивается до изоэнтропийной, какова будет конечная температура полосы?
Удельная теплоемкость при постоянной длине вычисляется Ct-1.2 J (степень (задачи, предложенной в тесте Оксфордского университета 1962 года).) И решение тоже.Термодинамическая идентичность Т ДС-дю-Ф дл. В результате f-dFjdl и термодинамическое уравнение состояния принимают вид: Итак, поскольку (dU / df) T = 0 [(di / d/) m = — (dUjdl) T (dHdf) T], U может быть только функцией T. a. работа, выполняемая при изотермическом напряжении, осуществляется в г г ’/ 21/2 / ГП’ — 2-4 Если вы представляете все значения системы CGS、 ХЛ 1×1 ЧПУ G 2002 году я 1002 1002 100П®м,Р7 ОП, 1.3.103.Зоопарк. + = D (7 = 0, поэтому поглощенное тепло 3 9. −3.9 J В =-А—0.93 коэф. 4.1 ОО В.
И так энтропийно равная работа f / d / = Cz (300-rKOH) Людмила Фирмаль
Если объединить последнее уравнение с уравнением состояния, то получим: Здесь Интеграл захватывается изэнтропиями. Изоэнтропийное отношение между I и T имеет следующий вид: 0 = сл ДТ-fdly Или dt. = 0、 Ct в T—f — — y-j = const、 = 100А = 1.3. 105 эрг / город. Да. / 2 I * Два Г / 2/2- Т. В. 300. Когда Ct = 1.2 J подставляется、 G = 300 ^ 0108 = 303,3°.
- 3.Излучение черного тела.Поскольку электромагнитное поле не является материальным, оно не может рассматриваться в рамках термодинамики.Но это не так.Замкнутые полости, поддерживаемые при постоянной температуре, постоянно заполняются электромагнитным излучением всех длин волн, которое может распространяться во всех directions.It оказывает давление на стенки полости и несет energy.It функция давления, так же, как температуры и volume.In короче говоря, такая замкнутая полость, заполненная излучением, как впервые установил Больцман (1889), представляет собой систему, в которой справедливо действуют законы термодинамики applied.
На этот раз учитель Больцмана Йозеф Штефан уже вывел из экспериментальных данных, что интенсивность излучения из отверстия в замкнутой полости, температура стенки которой везде одинакова, пропорциональна Т4.Из этого результата Больцман сделал правильный вывод, что плотность энергии и (T) равновесное излучение пропорциональны 4-степени температуры, и использовал термодинамику и электродинамику для получения этой зависимости.Максвелл, основываясь на своей теории электромагнетизма, установил, что давление, оказываемое полем изотропного излучения, составляет 73 градуса плотности энергии. р = 4″. Эта величина подставляется в термодинамическое уравнение состояния рффл. К Куда? дв)Т — [д’м)у = у(Т)в、 _ 1-дю 1
Мы получаем Или «»З ^ г«!’ И= То есть закон Стефана Больцмана.Коэффициент пропорциональности a явно является универсальной константой. Отсюда можно получить и другие термодинамические функции поля излучения. Объединение (5.20) и (5.24) с отношением Максвелла (5.16) (5.25) Например、 (5.26) Несовершенство классической теории проявлялось в том, что невозможно было предсказать распределение энергии излучения по разным длинам волн.
Это стало отправной точкой для революционного открытия Планка, который ввел гипотезу действия квантов.Но даже без квантовой теории можно кое-что сказать о распределении интенсивности так называемого излучения черного тела. В равновесном состоянии поле излучения может быть представлено набором стоячих волн в полости объема V. ВЗ, 3.、 (5.27) Тогда для образования стоячей волны необходимо, чтобы ее частота v удовлетворяла уравнению (5.28)) Где c-скорость света,/, t и n-целые числа.
Для макроскопического размера L, количество vLJc будет очень большим для всех длин волн c interest.So, число «собственных колебаний» (5.28), частота которых меньше v, GV пропорционально числу точек в сфере радиуса vL / c, имеющих целочисленные координаты f, m, n. (5.29) Г-ВВ. \ DOI выбрал для рассмотрения кубическую полость V, но, согласно немецкой теореме Вейля (1912), этот асимптотический результат не зависит от формы полости. Физический смысл целых чисел I, m и n таков:это число узлов стоячих волн вдоль соответствующих граней куба.
Они обладают следующими замечательными инвариантными свойствами: Если вы медленно меняете объем полости, то узловые грани каждой волны смещаются, а набор цифр f, m и n-нет changed.As для частоты собственных колебаний мы испытываем смещение, определяемое отношением к медленному расширению V — > V — \ — bV. (5.30)) Вы можете увидеть это, дифференцируя константы f, m и n(5.28).Таким образом, при постепенном изменении параметра V величина.
Собственная вибрация всех частот v (f, m, n).Это понятие играет очень важную роль в термодинамике.Это связано с постепенным изменением механических параметров-обратимым процессом теплоизоляции.Таким образом, существование параметрического инварианта в динамике системы подразумевает существование некоторого рода отношения, представляющего собой изоэнтропийное отношение между ее термодинамическими свойствами. parameters.In в рассматриваемом случае, согласно (5.26), изоэнтропийная зависимость поля излучения между объемом и температурой равна УУ3 = const. (5.32)) «)
Значение типа W называется параметрическим инвариантом. Людмила Фирмаль
Больцман использовал медленное термоизоляционное преобразование параметров механической системы, но важную роль в этом методе играет наличие P.It впервые был понят Эренфестом (см. Его обзорную статью[15]).Параметрические инварианты иногда называют адиабатическими инвариантами. Поэтому, если сравнить соотношение (5.31) с (5.32), то обратимое преобразование теплоизоляции будет (5.33) = Неизменный. Теперь мы можем сделать некоторые общие выводы о распределении лучистой энергии p (v)по различным частотам. (5.34))
Сначала подумайте об энтропии. Поскольку расширение спектра (например, с помощью решетки) является обратимым процессом, энтропия равна сумме вкладов каждого frequency.In кроме того, если адиабатический обратимый процесс 5 = const, то частота и температура могут попадать в отдельные члены этой суммы только в виде адиабатического инварианта v / 7, поэтому разложение 5 должно принимать вид: (5.35) Напишите на бланке разложение энергии Ф / = 2е(в. Т)(5.36) В. Согласно «(5.24) и (5.26)」 Ы-ы -, (5.37) Он приходит к выводу, что частное e (v, T) / T должно быть функцией v / 7 для каждого члена sum.So, тепловую энергию е, соответствующую собственным колебаниям, следует записать в виде: Е(В. р)= в /(- Ф); (5.38) Для этого ^ = С(т)•(5-39)
В соответствии с (5.29), плотность спектра настолько высока, что сумма может быть заменена интегралом. 2 = J dG ^ V J v2 dv. (5.40) В. Из соотношений (5.38) и (5.39) видно, что спектральное распределение энергии, фигурирующее в уравнении (5.34), имеет вид: п(п,Γ)= constvV(5-41) Максимальная интенсивность излучения черного тела определяется соотношением 3v2 / +(t»)/, = = 0 ’или константаг, (5.42) То есть пропорционально увеличению температуры она смещается на более высокую частоту (закон Вены).
Определение типа функции/является задачей статистической mechanics.It была эта проблема, которую оказалось невозможно решить с помощью классической теории.И наоборот, выводы термодинамики [соотношения (5.24), (5.26) и (5.41)] бесконечно применимы, поскольку они основаны только на понятиях 2 положений механики системы, то есть формулы Максвелла для радиационного давления (5.20) и параметрической инвариантности.
Сила в квантовой теории. Вызов.Если предположить, что величина энергии, соответствующая уровню энергии одночастичного одноатомного нерелятивистского разреженного газа, пропорциональна V〜v, то внутренняя энергия такого газа оказывается равной 3/2 ПВ. (Среди задач, предложенных на экзамене Оксфордского университета 1962 года) Решение.Энергия каждой молекулы Где/ — функция квантового числа, массы молекулы и др.Мы используем теорему квантовой механики следующим образом: Его функция/не изменяется, даже если изменяется громкость slowly.So, энергетический уровень изменяется медленно, но квантовое число не изменяется.Этот факт тесно связан с классической параметрической инвариантностью, рассматриваемой применительно к задаче излучения черного тела.
С тех пор Поскольку внутренняя энергия равна сумме 2 е, взятой для всех молекул, можно сделать вывод: Два / U = V 1X X функция адиабатического инварианта、 Или UV, 3 =постоянная вдоль равной энтропии.Отсюда、 Или ПВ ^ у、 Если вам нужно доказать.Заметим, что этот результат является более общим, чем уравнение состояния PV-RT. T = = не применяется вблизи 0.
Смотрите также:
| Преобразование переменных. Применение детерминантов якоби | Системы с переменной массой. Химический потенциал |
| Преобразования Лежандра | Примеры |

