Оглавление:









Примеры
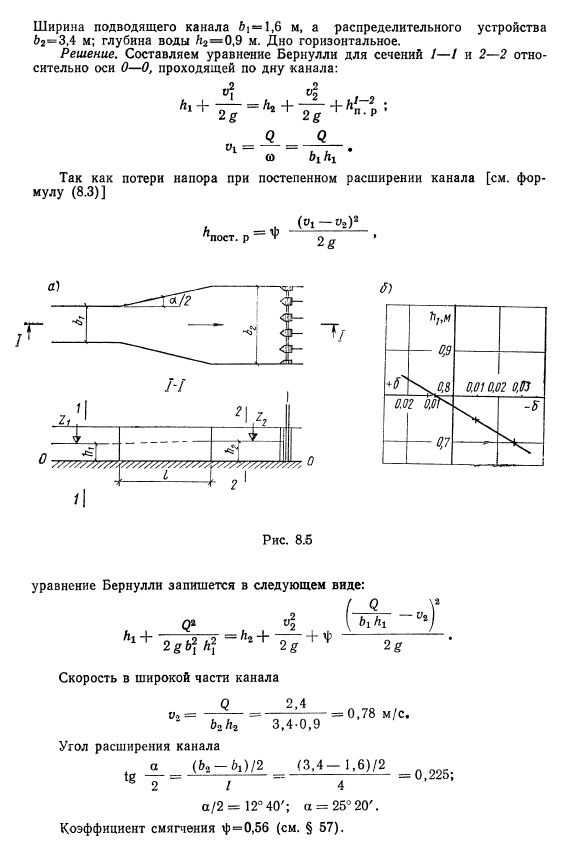
Примеры. Пример 8. 1. Определить отметку уровня воды 2 перед распределительным устройством (рис. 8. 5, а). Это постепенное расширение какао с длиной/ = 4 м и веткой на спине. Расход воды<2 = = 2, 4 м3 / с. Ответвление 22 затвора отметит уровень воды перед затвором= 87, 00 м. Ширина входного канала: 1 = 1, 6 м, распределительного устройства: 2 = 3, 4 м; глубина k2 = 0, 9 м. Дно горизонтальное. Решение. Составьте уравнения Бернулли в разделах 1-1 и 2-2 относительно оси 0-0, проходящей вдоль дна канала. O_ = _o_9 с БКГ* Потеря давления при постепенном расширении канала[ref.
Смотрите также:
Формула (8. 3 ] Уравнение Бернулли описывается следующим образом: Широкая скорость канала 2, 4 l2l2 3. 4-0. 9 Угол расширения канала a _ c, y / 2 _ 13. 4-1. 6) / ;ё2 / 4 а / 2 = 12°40 ′; а = 25°20 ’. Коэффициент релаксации равен f = 0, 56 (см. § 57). 173. Подставьте числа в уравнение Бернулли. Или к −0. 948+ 0. 067 + + 0. 051 = 0 Опишите полученное уравнение в виде: n −0. 948 + 0. 067 ax + 0. 051 = b. В результате расчетов получаем следующую формулу: когда]] = 0, 1 м 6 = −0, 027; + = 0, 75 м 6 = −0, 01; + = 0, 8 М 6 = 0, 008. По полученным данным составьте график b = / (+), из которого получится+ = 0, 78 м (рис. 8. 5. 6).
Смотрите также:
В основном, потери давления определяются силой трения движущейся воды о внутреннюю поверхность стенок трубопровода, которая имеет ту или иную шероховатость. Людмила Фирмаль
Это значение по умолчанию. Т = 2% -+ + + р = 67. 00-0. 9 + 0. 78 = 86. 88 м. Увеличение уровня происходит следующим образом: + +=0, 9-0, 78 = 0, 12 м = 12 см Пример 8. 2. Если ширина канала равна 6 = 1 м, то определяют перепад давления на повороте Открытого канала прямоугольного сечения. Радиус кривизны оси канала gf = 1, 5 м; глубина канала k-0, 7 м;угол поворота оси канала 0 = 120°; средняя скорость потока v = 0, 8 м/с. Решение. Найдите значение безразмерного параметра. / * с/ 6 = 1. 5; +6 = 0. 7; 6/180°= 0. 667 Радиус гидравлического канала Число Рейнольдса водных течений в канале y = m0_6 м2 / c.
Смотрите также:
Фильтрация. Основные определения.
По рисунку 8. 1. 6 rf / 6 = 1. 5 и+ 6 = 0. 7 находим значение коэффициента сопротивления в первом приближении:^ = 0. 15. Найденное значение относится к углу 0/180°= 0. 5. Из рисунка, g при 8. 1, + 6 = 0. 7 составляет 0/18°О, 5 1>-= 0. 28, а 0/180°= 0. 667 2; = 0. 33. Определить значение поправочного коэффициента f = 0, 33 / 0, 28 = 1, 18 и найти коэффициент лобового сопротивления во 2-м приближении. С = 1. 18-0. 15 = 0. 177 ′ 0. 18. Определяет потери давления на повороте канала: u2 0, 82 Л = Е = 0. 18 -! =0, 009 м < 0, 01 м 2§ 19. 6 Пример 8. 3 используйте следующие данные для определения потерь давления при повороте Открытого канала в трапециевидном сечении.
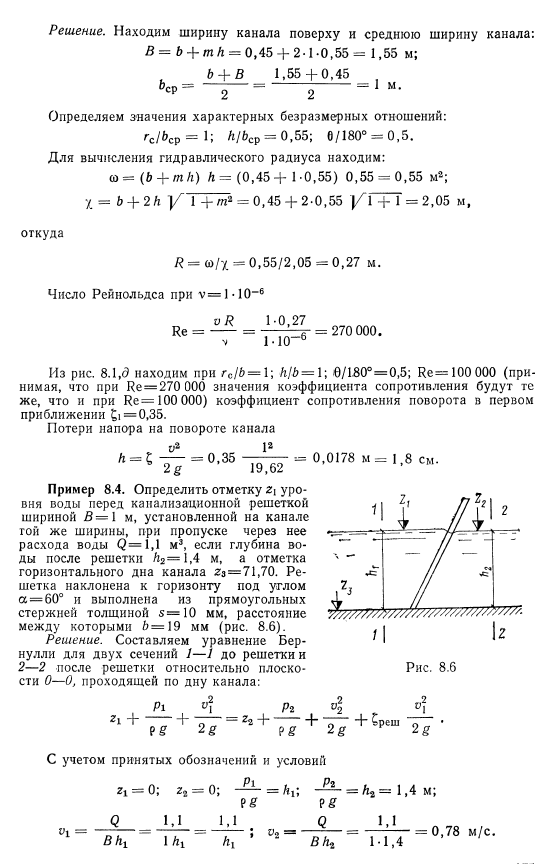
Коэффициент градиента m = 1; радиус кривизны оси канала gf = 1 м;глубина заполнения канала 6 = 0, 55 м; угол поворота оси канала 0 = 90°, средняя скорость потока v = 1 м / с. Сто семьдесят четыре Решение. Найдите ширину верхнего канала и среднюю ширину канала. Б = б + МК = 0. 45 + 2-1-0. 55 = 1, 55 м; Л + б 1. 55 + 0. 45 Лав = Р— = 1 м. Определите значение характеристической безразмерной зависимости. Rc1bcp = 1; / * / & СР. = 0, 55; 6/180° = 0, 5. Чтобы рассчитать гидравлический радиус, найдите следующее: Ко = (в + т) а=(0. 45 + 1-0. 55 0. 55 = 0. 55 м2. ; х = б + 2У 1 + Т2 = 0. 45 + 2-0. 55] l + 1 = 2, 05 м Откуда? = с / х = 0. 55 / 2. 05 = 0. 27 м.
Число Рейнольдса при y = l0-6 Рисунок 8. , q находится при rc / b = 1. H / l = 1; 0/180°= 0, 5; he = 100 000 (при условии, что he = 270 000 и значение коэффициента лобового сопротивления такое же, как he = 100 000) коэффициент сопротивления вращению в первом приближении равен^ 1 = 0, 35. Потеря канала Л =? = 0, 35 = 0, 0178 м = 1, 8 см2 / 19, 62 Пример 8. Если глубина воды после решетки 4 равна h2 = 1, 4 м, то определяют х отметку уровня воды перед решеткой канализации при b = 1 м, а при прохождении потока воды через канал такой же ширины<2 = 1, 1 м3, горизонтальную отметку дна канала 2z = 71, 70.
Если в качестве распределителя скоростей применена объемная решетка, проходные каналы которой не позволяют входящим в них струйкам перемешиваться, то коэффициент выравнивания потока за такой решеткой остается таким же, что и непосредственно перед ней. Людмила Фирмаль
- Решетка наклонена относительно горизонта под углом a = 60°и выполнена из прямоугольных брусков толщиной 5 = 10 мм, расстояние между которыми составляет b-19 мм (рис. 8. 6). Решение. Относительно плоскости 0-0, проходящей по дну канала, создадим уравнение Бернулли для 1 до решетки и 2-2 2 секций после решетки. С учетом принятых обозначений и условий Локальный коэффициент сопротивления решетки определяется по формуле (8. 6). Откуда? 19. 62 / г ’| −28. 1 + −0. 34 = 0. Если решить это уравнение графически, то оно составит 61, 4, 1, 42 м. Следовательно *! = 23 + ^ = 71. 70 + 1. 42 = 73. 12 м. ; 22 = Р8 + Л2 = 71. 70 + 1. 4 = 73. 10 м Уменьшение составляет 4 см.
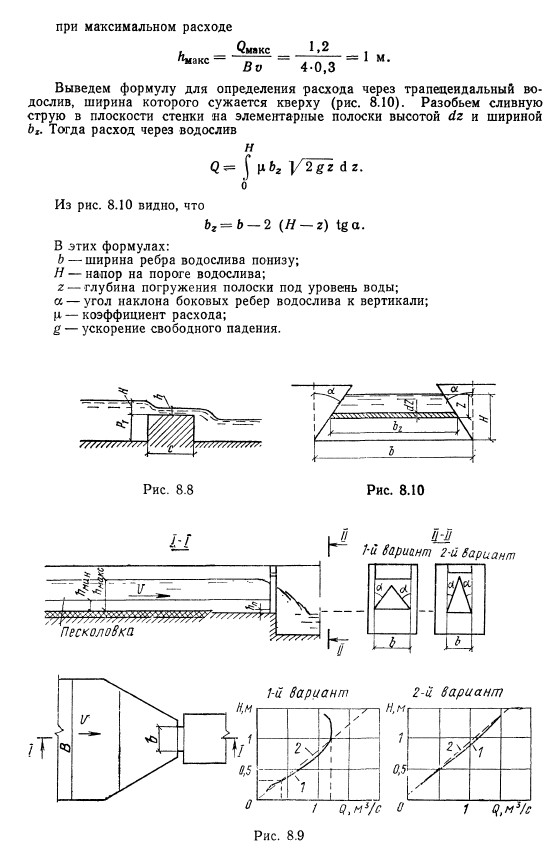
Пример: 8. 5 61 = 1 м ширина и уклон дна / установите лоток с критической глубиной на прямоугольном канале = = 0. 0013 для измерения расхода проходящей через него воды (см. Рис. 8. 3). Стены и дно канала покрыты кирпичом (/ г = 0, 017). Высота боковой стенки канала<2 = 1, 3 м. Максимальный расход воды в канале Оман= 1 м3 / s. To для обеспечения состояния свободного течения необходимо определить ширину горловины лотка В2. Решение. Определите глубину воды, которая будет равномерно двигаться в канале при максимальном расходе воды. Исходим из уравнения чезика 0 = СЮШ для нахождения различных глубин, пока не установим, что максимальный расход Омана= 1 м3 / с соответствует глубине/ 10 = 1 м.

