Пример существования бесчисленного множества положений равновесия

Пример существования бесчисленного множества положений равновесия

• Нить фиксируется в 2 точках Оси, и каждый элемент нити отталкивается от оси силой, пропорциональной его длине и расстоянию от этого элемента до оси. Проблема возникает, когда мы находим положение равновесия невесомой нити скакалки, которая вращается вокруг оси Ox с постоянной угловой скоростью. Поскольку все силы, действующие на нить, пересекают ось Ox, момент натяжения на этой оси постоянен вдоль всей нити. Однако, поскольку винт прикреплен к 2 точкам оси, момент натяжения на обоих концах равен zero. So этот момент становится нулевым везде И у нас есть откуда рфы dzЛ= 0, у м2, Юз Дж Где T константа. Это указывает на то, что равновесная фигура находится в плоскости, проходящей через ось Ox.

Используется в плоскости xy. Сила, действующая на элемент ds, тогда перпендикулярна оси Ox, пропорциональна ординате y и отталкивает Г ДС = п у ДС. Уравнение равновесия РФ 7 4Р = 0 РФ 7 + ш = 0 Из первого уравнения получаем T = A. где константа A всегда считается положительной путем подсчета дуги s направления. X увеличивается с. Присвойте значение этого T 2 му выражению и установите его JL 2 ДХ г а в ДС = ви + у 4x = Л Г. Довести до формы DX + M = O 1 + Г2 АИ Если мы интегрируем это уравнение 1 + 2 + 2 = a2 Левая сторона выражения положительна, поэтому константа должна быть положительной. Решите радикал, возведите уравнение в квадрат и замените у на его значение АЖД.

Для того чтобы по шести прямым можно было направить шесть сил, находящихся в равновесии, необходимо и достаточно, чтобы эти прямые принадлежали линейному комплексу. Людмила Фирмаль

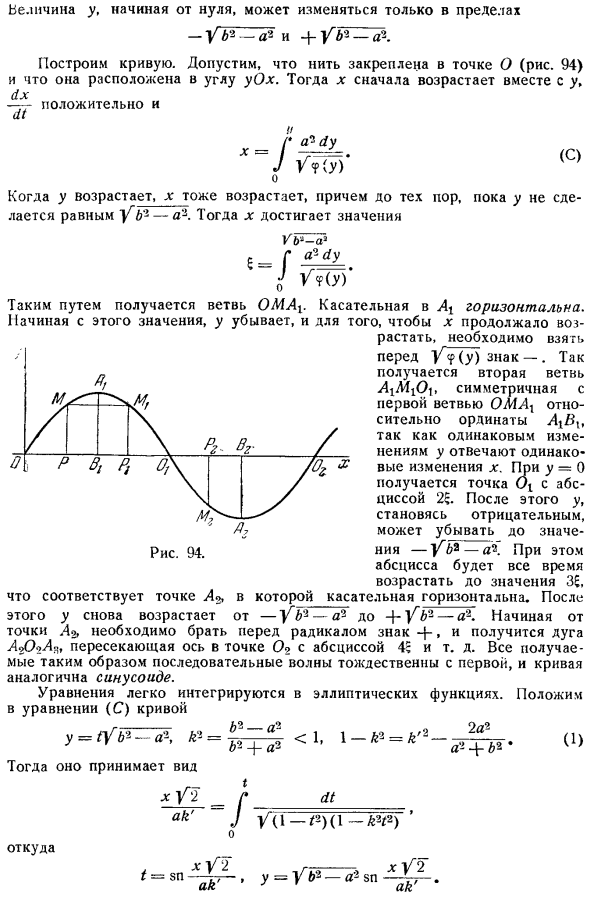
А4 дуплексный = В 2 У2 3. Поскольку нить соединена с осью Ox, если y = 0, то уравнение должно иметь действительное значение y. результат. 2 Если A p y представляет собой полином 4 го порядка под основанием, то сумма y, начиная с нуля Создайте кривую и поместите ее в dx Положительный и И 2. Предположим, что нить закреплена в точке О угол йех рис. 94.Затем x сначала увеличивается с y.

С когда y увеличивается, x также увеличивается, пока y не станет равным y a1.Тогда x достигнет значения Таким образом, ветвь OMAX извлекается. тангенс стеллаж для просушки в горизонтальном положении. Начиная с этого значения, y уменьшается, и для того, чтобы x продолжал увеличиваться, необходимо взять знак перед Y y .Это даст вам 2 ю ветвь yltefto. она симметрична с первой ветвью. такое же изменение в y соответствует одно и то же изменение в X, относительно оси ординат.

• Если y = 0, то точки берутся abscissa 26.Тогда y становится отрицательным и уменьшается до значения V a. В этом случае абсцисса всегда увеличивается до значения 36. Касательная горизонтальна. После YB2 a2 от 4 Y 2 a2.Если вы наберете символ f в передней части радикала, дуга будет отображаться Соответствует точке А Это Г снова растет Ло пойнт, ты должен взять В точке абсциссы 4 O2 пересекает ось LoOoL. Все последующие волны, полученные таким образом, идентичны первой, и кривая напоминает синусоиду.

Уравнения могут быть легко интегрированы Уравнение кривой C Год= Он принимает следующую форму Давай. В Эллиптическая функция. Поставь Откуда ЦДХ а 1 1 дифференциальный ds дуги кривой равен Подставляя 1 в это выражение, мы получаем следующие 2 выражения для абсциссы точки и длины X дуги OAX. Один Аляска 2 J 1 2 1 2 2 К Да. Один а 1 й А2 К В2 Дж Т Сцг СШ О 2 Потому что в случае точки Ar сумма t равна 1. Если заданы X и 6 и K должно быть больше, то дуга OA больше проекции OBit, а если k2 1, то константа имеет уникальную схему значений. Количество и Л2 X 6 1 З2 к2т Флорида. 3 если k2 = 0, то отношение справа равно нулю. 

Необходимо, следовательно, чтобы существовали две прямые, пересекающие одновременно все пять заданных прямых, или, на языке геометрии прямых, заданные пять прямых должны принадлежать линейной конгруенции. Людмила Фирмаль

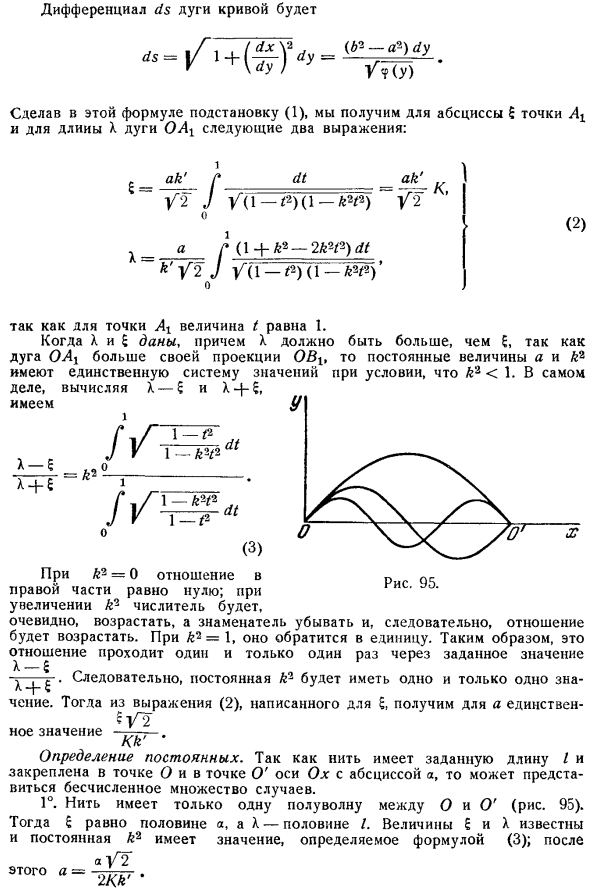
По мере увеличения k2 отношение увеличивается, потому что числитель явно увеличивается, а знаменатель уменьшается. если k2 = 1, то это unity. So, это соотношение проходит только 1 раз для определенного значения. Me. So, значение константы k2 равно только 1.Тогда из Формулы, описанной для 6 2, получим уникальное значение. Определение константы. Поскольку нить имеет заданную длину Z и закреплена на оси O и точке O оси Ox с горизонтальной осью a, может возникнуть множество случаев. 

Поток имеет только 1 полуволну между O и o рис. 95.Тогда 6 равно половине a, а X равно половине Z. величины и X известны, а константа k2 имеет значение, определяемое формулой 3. А после Г2 Итак, a = 2W 2.Нить имеет 2 полуволны между O и O .Тогда = Х = поскольку ХН К имеет то же значение, что и в предыдущем случае, и К А имеет то же значение г. А н а Затем Но… 2 2 4 л И затем 3. В общем случае, если нить имеет n полуволн между O Но…

Смотрите также:

Решение задач по теоретической механике

Определение постоянных	Равновесие нити на поверхности
Центральные силы	Естественные уравнения равновесия нити на поверхности