Пример решённой на заказ задачи №99.

Пример решённой на заказ задачи №99.

Исследовать функции и построить их графики:

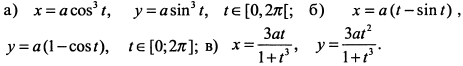
Решение:

а) Функции определены для любого значения 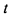. Поскольку функция 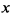четная, а 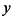нечетная, то график функции симметричен относительно оси ординат и начала координат, т. е. относительно координатных осей.

Полагая 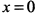, находим, что 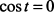и .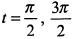

При этих значениях 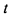из выражения 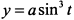находим, что .

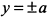Полагая 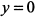, находим, что 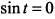и 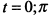. При этих значениях 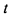из выражения 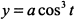находим, что 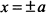. Таким образом, график функции пересекает координатные оси в точках .

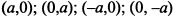Найдем производные 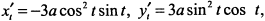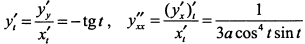. Из выражения для производной 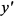определяем критические точки. При 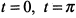производная равна нулю, а при 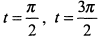не существует. Таким образом, область изменения параметра 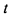разбивается на четыре интервала 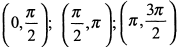и .

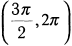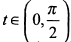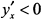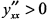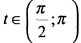
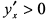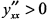При производная , а , т. е. функция убывает и график функции направлен выпуклостью вниз. При и , т. е. функция возрастает и график направлен выпуклостью вниз.

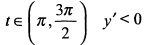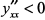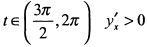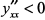При и , т. е. функция убывает и график направлен выпуклостью вверх. При , а , т. е. функция возрастает и график направлен выпуклостью вверх. Кстати, пользуясь симметрией графика функции, этот анализ можно было ограничить изменением параметра только одним интервалом, например, .

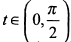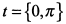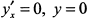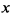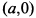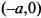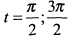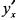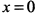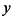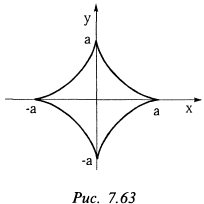
При производная и касательные совпадают с осью , т. е. точки и будут точками возврата. При производная не существует, а при , касательные совпадают с осью и точки 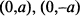будут также точками возврата. Учитывая все это, представим график функции (рис. 7.63). Полученная кривая представляет траекторию движения точки подвижного круга, катящегося изнутри по неподвижному кругу радиуса 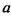, и называется астроидой.

б) Функция определена при любом значении параметра 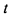из интервала 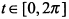. Найдем точки пересечения графика с осями координат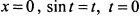. При . При 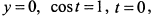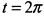. Отсюда следует, что кривая при 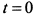проходит через начало координат, а при 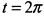пересекает ось 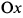в точке .

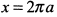Найдем производные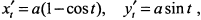

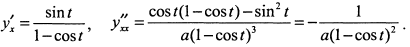
Приравнивая 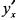к нулю, из уравнения 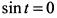находим значения параметра в критических точках 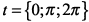. Первая производная не существует при 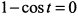, т. е. при значениях параметра 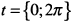. При переходе параметра через критические значения 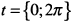, т. е. в окрестности 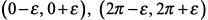, где 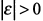, производная 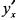меняет знак с минуса на плюс. Отсюда следует, что касательная к графику функции в точках 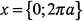параллельна ос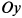и . При 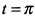вторая производная 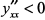, т. е. точка 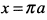точка максимума функции 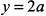. Более того, поскольку 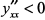на всем интервале 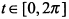, то кривая на этом интервале выпукла вверх.

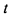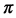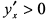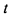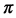При изменении от 0 до производная , следовательно, кривая возрастает. При изменении от до 2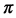 производная 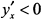, следовательно, кривая убывает. Все сказанное позволяет представить график в виде (рис. 7.64). Полученная кривая представляет траекторию точки круга радиуса 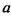катящегося без скольжения по прямой 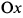за время одного оборота круга и называется циклоидой.

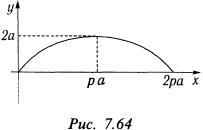
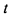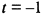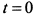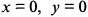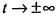в) Функция определена при всех значениях , кроме . При координаты и при координаты 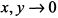, т. е. начало координат служит особой точкой и в нем кривая сама себя пересекает.

Найдем наклонную асимптоту. Угловой коэффициент равен

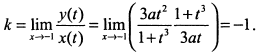
Параметр

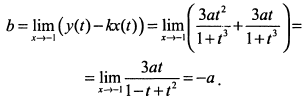
Отсюда уравнение асимптоты .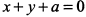

При изменении 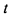от 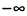до -1, точка 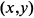из начала координат удаляется в бесконечность, причем значения 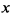— положительны, а 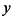— отрицательны, т. е. ограничены асимптотой, расположенной в четвертом квадранте.

При изменении 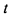от -1 до 0 точка 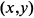из бесконечности возвращается к началу координат, причем значения 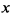— отрицательны, а 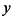— положительны, т. е. ограничены асимптотой, расположенной во втором квадранте. При изменении 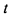от 0 до 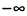точка описывает против часовой стрелки петлю, расположенную, судя по значениям 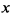, , 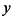в первом квадранте.

Обозначая 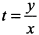, нетрудно перейти к уравнению функции в неявном виде 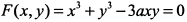. Находим производные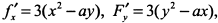 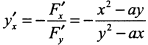. Приравнивая 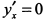и решая это уравнение совместно с уравнением 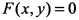, находим критические точк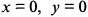и и 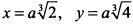. Вычислим 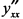при 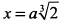по формуле 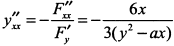. Так как в исследуемой точке 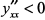, то это точка максимума .

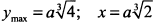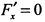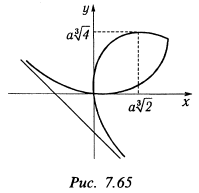
В точке (0,0) и 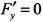, поэтому можно утверждать, что касательными в этой точке служат оси координат. Учитывая все это, представим график функции (рис. 7.65). Полученная кривая называется декартовым листом.

На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:

Заказать решение заданий по высшей математике

Для вас подобрала похожие примеры с решением возможно они вам пригодится:

Пример решённой на заказ задачи №95.

Пример решённой на заказ задачи №97.

Пример решённой на заказ задачи №102.

Пример решённой на заказ задачи №104.