Пример решённой на заказ задачи №95.
Исследовать направление выпуклости и найти точки перегиба кривой: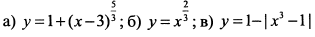 
.
Решение:
а) Находим: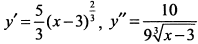 
. Вторая производная не существует в точке 
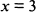и не обращается в нуль ни при каких значениях 
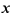. При переходе через точку 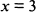вторая производная меняет знак с минуса на плюс, следовательно, точка (3,1) является точкой перегиба. Поскольку при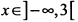 
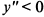, то в этом интервале кривая выпукла вверх. При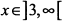 
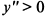, следовательно, кривая выпукла вниз.
б) Найдем вторую производную: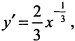 
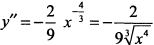. Производная 
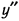нигде в нуль не обращается. При 
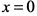вторая производная не существует. При переходе через точку 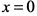вторая производная знака не меняет: 
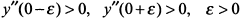. При 
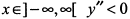, следовательно, кривая выпукла вверх на всей числовой оси.
в) Находим точки 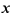, в которых 
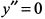или не существует: 
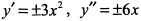, где знак плюс соответствует значениям 
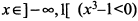, а минус—
.
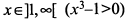Поскольку при 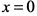вторая производная 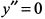, а при 
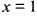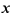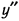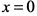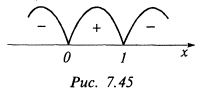
не существует, то эти значения могут быть абсциссами точек перегиба. Знак слева и справа от точек и 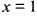показан на рис. 7.45. Так как 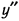при переходе через точк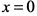и и 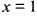меняет знаки, то 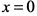и 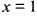— абсциссы точек перегиба. При 
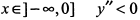— кривая выпукла вверх, при 
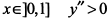— кривая выпукла вниз, при 
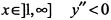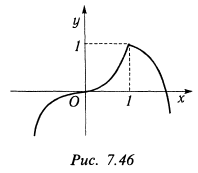
— кривая выпукла вверх. Определяя ординаты точек перегиба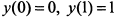 
, строим кривую (рис. 7.46).
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №91. |
| Пример решённой на заказ задачи №93. |
| Пример решённой на заказ задачи №97. |
| Пример решённой на заказ задачи №99. |
