Пример решённой на заказ задачи №91.
Найти наибольшее и наименьшее значения функций:
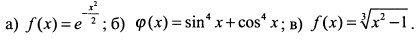
а) Функция определена на всей числовой оси, а изменение аргумента 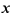 не ограничено каким-либо отрезком, поэтому следует исследовать значения функции при
не ограничено каким-либо отрезком, поэтому следует исследовать значения функции при 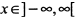 .
.
Вычисляем производную 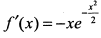 и, приравнивая ее к нулю, находим критическую точку
и, приравнивая ее к нулю, находим критическую точку 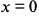 . При переходе через эту точку производная функции меняет знак с + на — , следовательно,
. При переходе через эту точку производная функции меняет знак с + на — , следовательно, 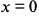 точка максимума
точка максимума 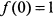 . При
. При 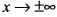 функция бесконечно убывает, но наименьшего значения не имеет (рис. 7.31).
функция бесконечно убывает, но наименьшего значения не имеет (рис. 7.31).
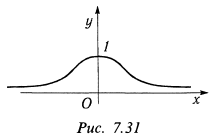
б) Функция определена на всей числовой оси. Изменение аргумента не ограничено отрезком, поэтому рассмотрим значения функции при 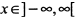 .
.
Находим производную  и приравниваем ее к нулю
и приравниваем ее к нулю 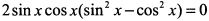 , откуда
, откуда 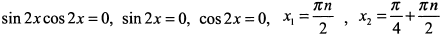 . Подставляя найденные критические точки в функцию находим, что при
. Подставляя найденные критические точки в функцию находим, что при 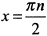
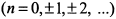 функция имеет наибольшие значения равные единице, а при
функция имеет наибольшие значения равные единице, а при 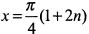
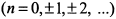 — наименьшие значения равные
— наименьшие значения равные 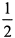 .
.
в) Функция задана и определена на всей числовой оси. Исследуем значения функции при 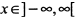 . Найдем производную
. Найдем производную 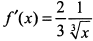 . В точке
. В точке 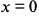 производная не существует. Значение функции при
производная не существует. Значение функции при 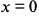 равно -1. При
равно -1. При 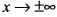 функция не ограничено возрастает.
функция не ограничено возрастает.
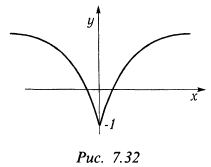
Следовательно, наименьшее значение функции будет 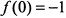 , а наибольшего значения функция не имеет (рис. 7.32).
, а наибольшего значения функция не имеет (рис. 7.32).
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №87. |
| Пример решённой на заказ задачи №89. |
| Пример решённой на заказ задачи №93. |
| Пример решённой на заказ задачи №95. |

