Пример решённой на заказ задачи №87.
Доказать справедливость неравенств:
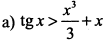 при
при 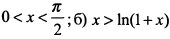 при
при 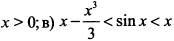 при
при 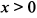 .
.
Решение:
а) Найдем производную функции 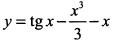 для указанных значений
для указанных значений 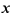 :
: 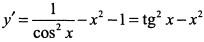 .
.
Поскольку 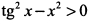 , так как
, так как 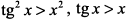 , тo
, тo 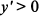 и функция возрастает, откуда
и функция возрастает, откуда 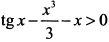 или
или 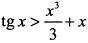 .
.
б) Найдем производную функции 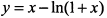 :
: 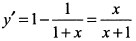 . При
. При 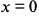 функция имеет минимум, а при
функция имеет минимум, а при 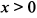 ,
, 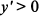 и функция возрастает. Следовательно,
и функция возрастает. Следовательно, 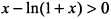 , откуда
, откуда 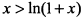 .
.
в) Рассмотрим систему неравенств
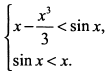
Введем функции  и найдем их производные
и найдем их производные 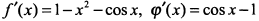 . При
. При 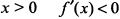 , так как
, так как 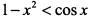 , и
, и 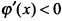 или равна нулю для значений
или равна нулю для значений 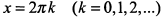 , так как
, так как 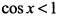 . Функции убывающие, следовательно
. Функции убывающие, следовательно 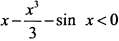 и
и 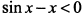 , откуда
, откуда  .
.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №83. |
| Пример решённой на заказ задачи №85. |
| Пример решённой на заказ задачи №89. |
| Пример решённой на заказ задачи №91. |

