Пример решённой на заказ задачи №83.
Проверить справедливость теоремы Лагранжа для функций: 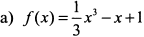 на [0,1];
на [0,1]; 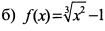 на [-1,1]. Если теорема применима, то найти точку
на [-1,1]. Если теорема применима, то найти точку 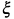 .
.
Решение:
а) Данная функция на отрезке [0,1] непрерывна и имеет конечную производную 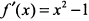 . Следовательно, условия теоремы Лагранжа выполняются. Точку
. Следовательно, условия теоремы Лагранжа выполняются. Точку 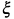 найдем из формулы конечных приращений
найдем из формулы конечных приращений 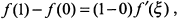
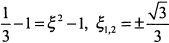 . Поскольку
. Поскольку 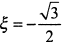 не принадлежит отрезку [0,1], то искомое значение
не принадлежит отрезку [0,1], то искомое значение 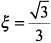 .
.
б) Функция непрерывна на отрезке [-1,1] и имеет производную 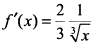 . Поскольку производная в точке
. Поскольку производная в точке 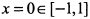 не существует, то теорема Лагранжа к данной функции не применима.
не существует, то теорема Лагранжа к данной функции не применима.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №79. |
| Пример решённой на заказ задачи №81. |
| Пример решённой на заказ задачи №85. |
| Пример решённой на заказ задачи №87. |

