Пример решённой на заказ задачи №77.
Найти производные указанного порядка: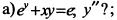 
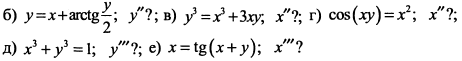
Решение:
а) Дифференцируем правую и левую часть по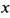 
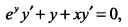
откуда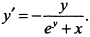 
Дифференцируем еще один раз по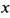
Подставляя в последнее выражение значение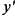 
, получим
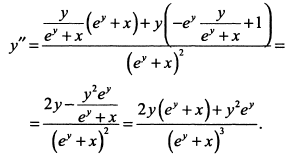
б) Дифференцируем обе части по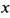
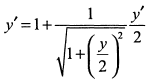
откуда 
Дифференцируем еще раз по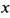
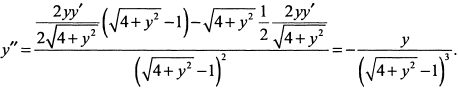
в) Дифференцируем правую и левую часть по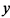 
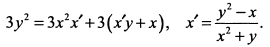
Дифференцируем еще раз по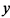
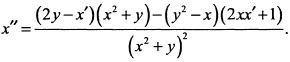
Подставляя в последнее выражение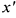 
, получим
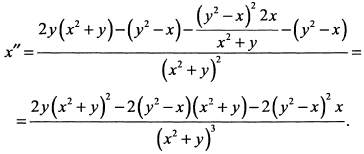
г) Дифференцируем обе части по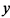
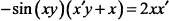, откуда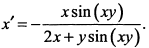 
Дифференцируем еще раз по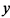
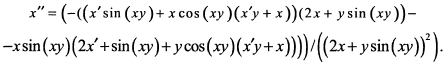
д) Дифференцируем обе части по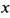
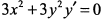, откуда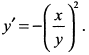 
Дифференцируем еще раз по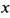
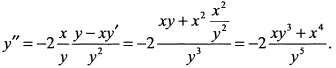
Для нахождения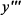 
дифференцируем еще один раз по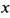
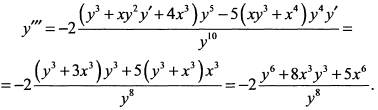
е) Дифференцируем обе части по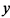
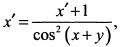
откуда
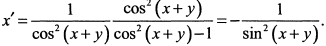
Дифференцируем еще раз по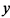
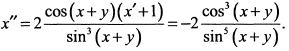
Дифференцируя еще раз по 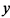, окончательно получим
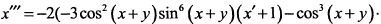
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №73. |
| Пример решённой на заказ задачи №75. |
| Пример решённой на заказ задачи №79. |
| Пример решённой на заказ задачи №81. |
