Пример решённой на заказ задачи №61.
Показать, что векторы 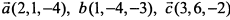 образуют базис пространства и найти координаты вектора
образуют базис пространства и найти координаты вектора 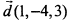 в этом базисе.
в этом базисе.
Решение:
Составим матрицу из компонент векторов 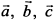 , приняв их за столбцы
, приняв их за столбцы
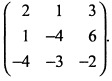
Для определения ранга этой матрицы вычислим определитель
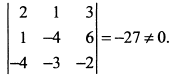
Отсюда следует, что ранг матрицы 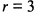 . Так как ранг матрицы равен числу векторов, то они линейно независимы, а в трехмерном пространстве любые три линейно независимых вектора образуют базис.
. Так как ранг матрицы равен числу векторов, то они линейно независимы, а в трехмерном пространстве любые три линейно независимых вектора образуют базис.
Обозначив координаты вектора 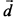 в базисе
в базисе 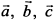 , через
, через 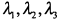 , получим векторное уравнение
, получим векторное уравнение
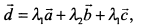
которое равносильно системе трех уравнений
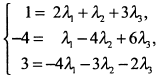
Решаем эту систему относительно 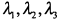 . По формулам Крамера
. По формулам Крамера  .
.
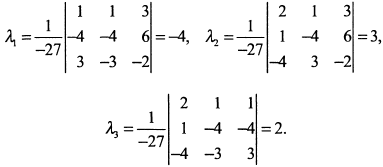
Координаты вектора 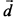 в базисе
в базисе 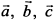 будут:
будут: 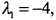
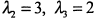 , т. е.
, т. е. 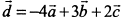 .
.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №57. |
| Пример решённой на заказ задачи №59. |
| Пример решённой на заказ задачи №67. |
| Пример решённой на заказ задачи №69. |

