Пример решённой на заказ задачи №53.
Установить поверхность, определяемую уравнением:
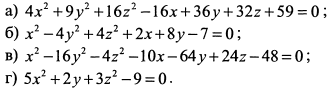
Решение:
а) Поскольку уравнение не содержит произведений координат, то приведение его к простейшему виду осуществляется посредством параллельного переноса. Выделим полные квадраты
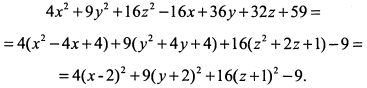
Полагая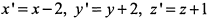 
, находим, что в системе координат 
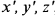, смещенной относительно системы 
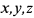параллельным переносом начала в точку с координатами 
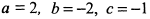данная поверхность имеет простейшее уравнение вида
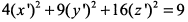или 
.
Таким образом, данное уравнение определяет эллипсоид (1) с центром в точке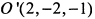 
и полуосями 
.
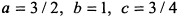б) Уравнение не содержит произведений координат. Преобразуем левую часть до полных квадратов
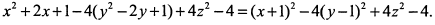
Полагая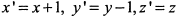 
, получим уравнение поверхности в системе координат 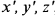, смещенной относительно системы 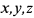параллельным переносом начала в точку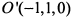 
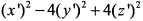или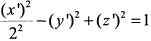 
.
Поскольку в этом уравнении коэффициенты пр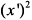и 
и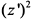 
положительные, а при 
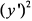— отрицательный, то данное уравнение определяет однополостный гиперболоид (3), расположенный вдоль оси 
.
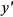в) Преобразуя левую часть до полных квадратов, приходим к уравнению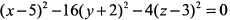 
, из которого после замены 
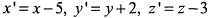получим уравнение поверхности в системе координат 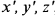смещенной относительно системы 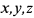параллельным переносом начала координат в точку (5,-2,3)
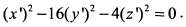
Поскольку в этом уравнении свободный член равен нулю и коэффициенты при квадратах координат разных знаков, то данное уравнение определяет конус второго порядка (11) с осью вдоль оси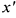 
и вершиной в точке (5,-2,3).
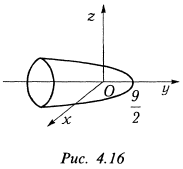
г) Данное уравнение содержит две координаты во второй степени и одну в первой, следовательно, уравнение определяет эллиптический парболоид (5). Переписывая его в виде 
, заключаем, что вершина параболоида расположена в точке с координатами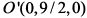 
и его полость обращена в сторону отрицательных значений 
. Если обозначить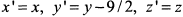 
, то получим каноническое уравнение параболоида (рис. 4.16)
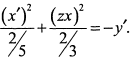
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №49. |
| Пример решённой на заказ задачи №51. |
| Пример решённой на заказ задачи №55. |
| Пример решённой на заказ задачи №57. |
