Пример решённой на заказ задачи №45.
Найти уравнения кривых в прямоугольных координатах: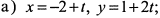 
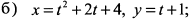
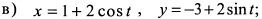
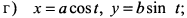
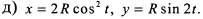
Решение:
а) Найдем из первого уравнения параметр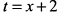 
и исключим его из второго уравнения. Тогда получим 
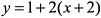или 
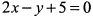. Это уравнение прямой.
б) Представим первое уравнение в виде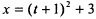 
, тогда 
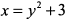. Это уравнение параболы с вершиной, смещенной на три единицы по оси 
.
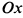в) Разрешим уравнения относительно тригонометрических функций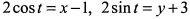 
. Возведем в квадрат и сложим 
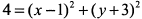. Кривая представляет окружность с центром в точке (1; -3) и радиусом равным 2.
г) Разделим правые части на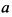 
и 
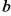, возведем выражения в квадрат и сложим 
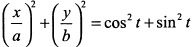или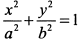 
. Это уравнение эллипса.
д) Возведем второе выражение в квадрат и преобразуем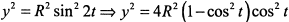 
. Найдем из первого уравнения 
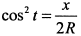и подставим, тогда
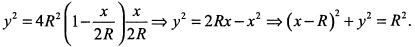
Уравнение окружности с центром, смещенным по оси 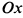на радиус 
.
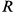На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №41.2. |
| Пример решённой на заказ задачи №43. |
| Пример решённой на заказ задачи №47. |
| Пример решённой на заказ задачи №49. |
