Пример решённой на заказ задачи №36.
Найти прямую, параллельную прямым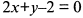 
и 
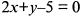, расположенную между ними и делящую расстояние между ними в отношении 1:5.
Решение:
Возьмем на первой прямой точку 
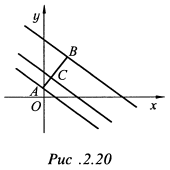
, абсцисса которой равна, например, нулю. Тогда ордината точки из уравнения прямой равна 2. Проведем из этой точки перпендикуляр до пересечения со второй прямой в точке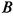 
(рис. 2.20).
Угловой коэффициент прямой равен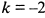 
, следовательно, угловой коэффициент перпендикуляра 
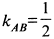. Подставляя его и координаты точки в уравнение пучка прямых (8), находим уравнение перпендикуляра 
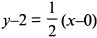или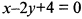 
.
Решая уравнение перпендикуляра совместно с уравнением второй прямой, находим точку их пересечения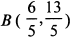 
.
Пусть точка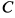 
делит отрезок 
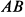в отношении 
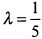, тогда ее координаты
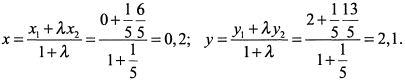
Так как искомая прямая параллельна данным прямым, то ее угловой коэффициент 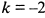. Подставляя его и координаты точки 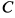в уравнение пучка прямых, находим уравнение искомой прямой 
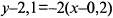или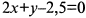 
.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №32. |
| Пример решённой на заказ задачи №34. |
| Пример решённой на заказ задачи №38. |
| Пример решённой на заказ задачи №40. |
