Пример решённой на заказ задачи №174.
Найти площадь, ограниченную: а) эллипсом 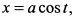
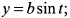 б) одной аркой циклоиды
б) одной аркой циклоиды 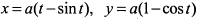 и осью
и осью 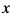 ; в) астроидой
; в) астроидой 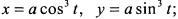 г) кривой
г) кривой 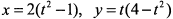 .
.
Решение:
а) Оси координат делят эллипс на четыре одинаковые части (рис. 3.32). Найдем площадь, расположенную в первом квадранте
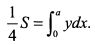
Поскольку эллипс задан уравнениями в параметрическом виде, то преобразуем интеграл к переменной 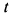 . При
. При 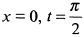 , а при
, а при 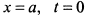 . Таким образом
. Таким образом
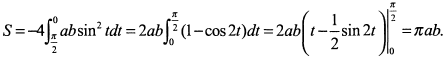
б) При 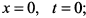 при
при 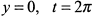 (рис. 3.67). По формуле (6) имеем
(рис. 3.67). По формуле (6) имеем
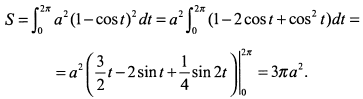
в) Оси координат делят астроиду на четыре одинаковые части (рис. 7.63). Найдем площадь, расположенную в первом квадранте. При 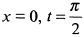 ; при
; при 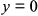 ,
, 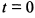 . Отсюда по формуле (6) вся площадь будет равна
. Отсюда по формуле (6) вся площадь будет равна
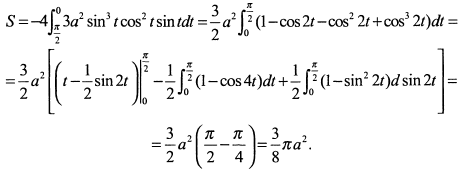
г) Найдем точки пересечения кривой с осями координат. Если 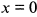 , то (
, то (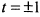 ; если
; если 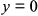 , то
, то 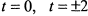 . Отсюда получим следующие точки: при
. Отсюда получим следующие точки: при 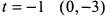 , при
, при 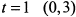 ; при
; при 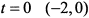 ; при
; при 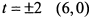 .
.
Если 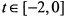 , то
, то 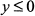 ; если
; если 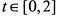 , то
, то 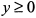 . Точка (6,0) является точкой самосопряжения кривой. Следовательно, кривая имеет форму петли (рис. 12.14).
. Точка (6,0) является точкой самосопряжения кривой. Следовательно, кривая имеет форму петли (рис. 12.14).
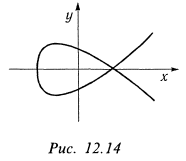
Вследствие симметрии фигуры относительно оси 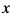 , достаточно найти половину площади; тогда вся площадь по формуле (6) будет равна
, достаточно найти половину площади; тогда вся площадь по формуле (6) будет равна
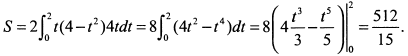
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №169. |
| Пример решённой на заказ задачи №171. |
| Пример решённой на заказ задачи №176. |
| Пример решённой на заказ задачи №178. |

