Пример решённой на заказ задачи №171.
Вычислить интегралы:
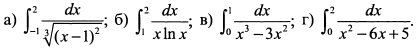
Решение:
а) Поскольку в точке 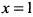 , принадлежащей промежутку интегрирования, функция терпит разрыв, то интеграл относится к несобственным интегралам второго рода и вычисляется по формуле (4)
, принадлежащей промежутку интегрирования, функция терпит разрыв, то интеграл относится к несобственным интегралам второго рода и вычисляется по формуле (4)
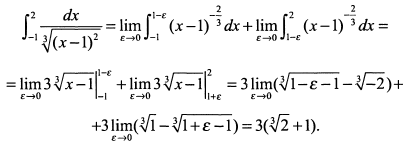
б) Подынтегральная функция терпит разрыв в точке 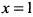 , т. е. на конце промежутка [1,2]. Следовательно, интеграл относится к несобственным интегралам второго рода и вычисляется
, т. е. на конце промежутка [1,2]. Следовательно, интеграл относится к несобственным интегралам второго рода и вычисляется

в) При 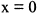 подынтегральная функция обращается в бесконечность, во всех остальных точках промежутка [0,1] она непрерывна. Следовательно, имеем
подынтегральная функция обращается в бесконечность, во всех остальных точках промежутка [0,1] она непрерывна. Следовательно, имеем
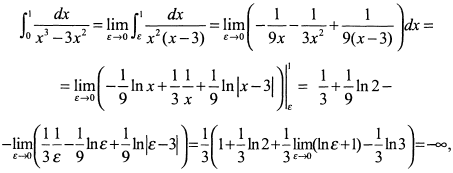
т. е. интеграл расходится.
г) Подынтегральная функция непрерывна в промежутке [0,2] за исключением точки 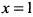 , в которой она терпит разрыв. Следовательно,
, в которой она терпит разрыв. Следовательно,
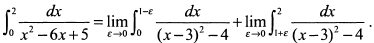
Первый интеграл равен
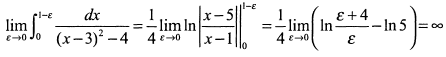
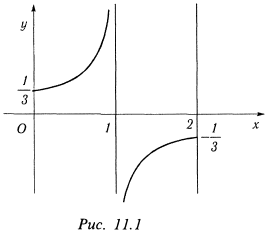
и представляет неограниченную площадь криволинейной трапеции
(рис. 11.1), ограниченную осью 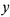 , кривой
, кривой 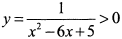 на данном промежутке, осью абсцисс и вертикальной асимптотой
на данном промежутке, осью абсцисс и вертикальной асимптотой 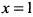 .
.
Второй интеграл равен
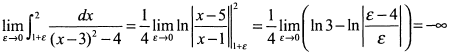
и представляет неограниченную площадь криволинейной трапеции(рис. 11.1), ограниченную осью 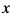 , прямой
, прямой 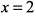 , вертикальной асимптотой
, вертикальной асимптотой 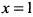 и функцией
и функцией 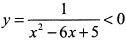 на данном промежутке.
на данном промежутке.
Данный интеграл представляет два расходящихся интеграла, т. е. расходится.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №167. |
| Пример решённой на заказ задачи №169. |
| Пример решённой на заказ задачи №174. |
| Пример решённой на заказ задачи №176. |

