Пример решённой на заказ задачи №132.
Показать, что особые точки кривой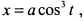 
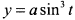есть точки возврата первого рода.
Решение:
Найдём первые производные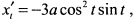 
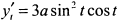. Приравнивая их нулю, получим четыре особые точки 
.
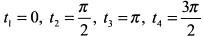Вычислим вторые производные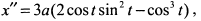 
.
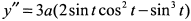Поскольку в особых точках вторая производная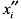 
или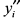 
отлична от нуля, то налицо точки возврата. Найдём третьи производные 
.
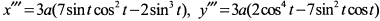Так как в особых точках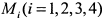 
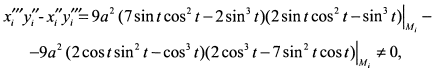
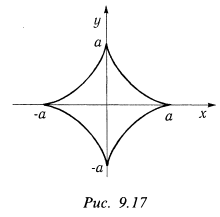
то это точки возврата первого рода. Нетрудно заметить, что заданная кривая есть астроида (рис. 9.17 ), декартовые координаты точек возврата которой, соответственно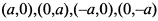 
.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №128. |
| Пример решённой на заказ задачи №130. |
| Пример решённой на заказ задачи №134. |
| Пример решённой на заказ задачи №136. |
