Пример решённой на заказ задачи №124.
В эллипсоид вписать прямоугольный параллелепипед наибольшего объема.
Решение:
В силу симметрии заданных геометрических фигур достаточно исследовать на условный экстремум функцию объема 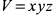 , т. е. объема параллелепипеда расположенного в первом октанте. Учитывая, что уравнение связи есть уравнение эллипсоида, составим функцию Лагранжа
, т. е. объема параллелепипеда расположенного в первом октанте. Учитывая, что уравнение связи есть уравнение эллипсоида, составим функцию Лагранжа
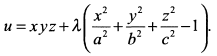
Находим частные производные 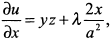
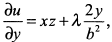
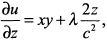 тогда необходимое условие экстремума будет
тогда необходимое условие экстремума будет
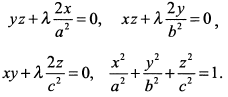
Решая эту систему, будем иметь 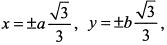
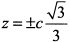 . Поскольку рассматривается только первый октант, то условный экстремум будет в точке с координатами
. Поскольку рассматривается только первый октант, то условный экстремум будет в точке с координатами 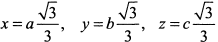 . Отсюда следует, что прямоугольный параллелепипед наибольшего объема имеет измерения
. Отсюда следует, что прямоугольный параллелепипед наибольшего объема имеет измерения 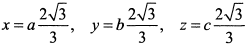 .
.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №120. |
| Пример решённой на заказ задачи №122. |
| Пример решённой на заказ задачи №126. |
| Пример решённой на заказ задачи №128. |

