Пример решённой на заказ задачи №122.
Представить положительное число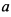 
в виде произведения четырех положительных множителей так, чтобы их сумма была наименьшей.
Решение:
По условию задачи требуется найти наименьшее значение суммы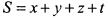 
при условии, что 
. Представляя 
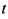в виде 
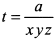и подставляя это выражение в сумму, будем иметь 
, т. е. функцию трех переменных, причем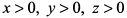 
. Найдем стационарную точку.
Для этого вычислим производные и приравняем их к нулю
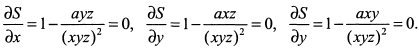
Решая эту систему уравнений, находим, что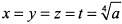 
, т. е. все множители равны. Докажем, что в этой точке сумма принимает максимальное значение. Действительно, при приближении какой-либо переменной к пограничным значениям 
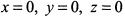равно как и при удалении в бесконечность, функция суммы 
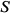бесконечно возрастает. Следовательно, найденная стационарная точка будет той точкой, в которой сумма 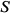будет наименьшей.
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №118. |
| Пример решённой на заказ задачи №120. |
| Пример решённой на заказ задачи №124. |
| Пример решённой на заказ задачи №126. |
