Пример решения заказа контрольной работы №95.
Исследуйте ряд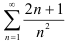 
на сходимость, применяя признак сравнения.
Решение:
Рассмотрим ряд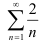 
. Поскольку он получается из расходящегося гармонического ряда 
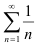умножением на 2, то, по свойству числовых рядов (свойство 2), он расходится. Сравним исследуемым ряд с рядом 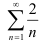. Имеем:
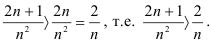
Таким образом, общий член исследуемого ряда больше общего члена расходящегося ряда.
Следовательно, по признаку сравнения, ряд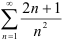 
расходится.
Ответ: 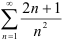расходится.
В отличие от признака сравнения, где многое зависит от догадки и запаса «эталонных» рядов, признак Даламбера часто позволяет исследовать сходимость ряда, проделав лишь некоторые операции над ним.
Признак Даламбера: Пусть дан положительный числовой ряд 
, и существует конечный или бесконечный предел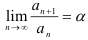 
. Тогда:
• если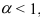 
, то ряд 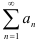сходится;
• если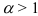 
, то ряд 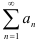расходится;
• если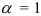 
, то признак не применяется (вопрос о сходимости ряда остается открытым).
Исследовать ряд 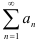на сходимость но признаку Даламбера удобно по следующему алгоритму:
- найти
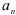; - найти
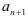; - найти
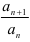
- найти предел отношения на бесконечности
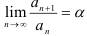и проанализировать полученное значение:
если 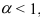, то ряд 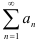сходится;
если 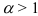, то ряд 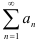расходится;
если 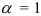, то признак Даламбера ответа не дает (требуется дополнительное исследование). Рассмотрим пример использования признака Даламбера для исследования сходимости положительных рядов.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №90. |
| Пример решения заказа контрольной работы №92. |
| Пример решения заказа контрольной работы №96. |
| Пример решения заказа контрольной работы №108. |
