Пример решения заказа контрольной работы №90.
Найдите объем цилиндрического тела, ограниченного сверху поверхностью 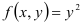 , снизу — областью
, снизу — областью 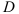 плоскости
плоскости 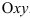 , представляющей собой прямоугольный треугольник, образованный координатными осями и прямой
, представляющей собой прямоугольный треугольник, образованный координатными осями и прямой
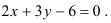
Решение:
В силу геометрического смысла двойного интеграла от неотрицательной функции, для нахождения объёма цилиндрического тела будем использовать формулу:
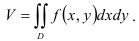
Вычислим двойной интеграл
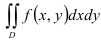
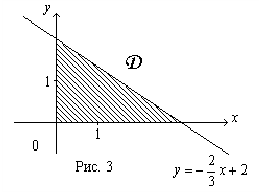
по области 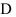 . Для этого построим область интегрирования
. Для этого построим область интегрирования 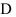 в прямоугольной декартовой системе координат на плоскости. Составим уравнение прямой
в прямоугольной декартовой системе координат на плоскости. Составим уравнение прямой
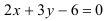
с угловым коэффициентом:
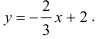
Построим эту прямую по двум точкам:
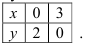
Изображенная на рисунке область интегрирования  (рис.3) является криволинейной областью. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
(рис.3) является криволинейной областью. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
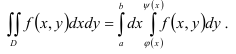
В нашем случае
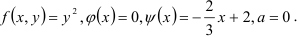
Найдем 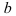 как абсциссу точки пересечения прямой
как абсциссу точки пересечения прямой 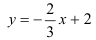 с осью
с осью 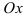 , решив уравнение:
, решив уравнение: 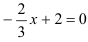 .
.
Получим 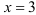 , значит
, значит 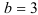 .
.
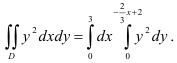
Вычислим полученный повторный интеграл:
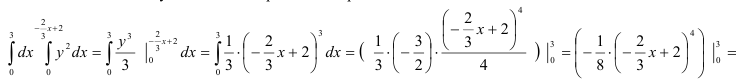
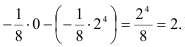
В итоге
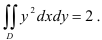
Следовательно,
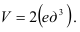
Ответ:
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №81. |
| Пример решения заказа контрольной работы №88. |
| Пример решения заказа контрольной работы №92. |
| Пример решения заказа контрольной работы №95. |

