Пример решения заказа контрольной работы №88.

Пример решения заказа контрольной работы №88.

Вычислите двойной интеграл

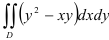
по области 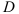, ограниченной линиями

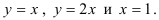
Решение:

Воспользуемся алгоритмом вычисления двойного интеграла.

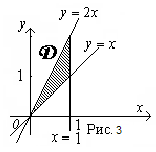
1) Построим область интегрирования D в прямоугольной декартовой системе координат на плоскости (рис.3) . Линия, задаваемая уравнением 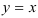— прямая, являющаяся биссектрисой I и III координатных углов.

Линия, задаваемая уравнением 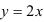прямая. Построим ее по двум точкам:

Линия, задаваемая уравнением 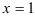, — прямая, параллельная оси 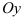и проходящая через точку (1;0).

В итоге, область интегрирования 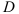обозначена на рис. 29.5. штриховкой.

2) Область интегрирования 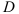является криволинейной областью. Для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:

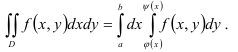
В нашем случае

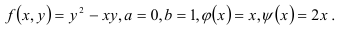
Следовательно,

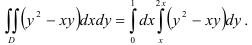
3) Вычислим полученный повторный интеграл:

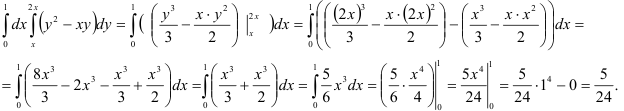
Таким образом, окончательно имеем:

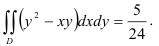
Ответ:

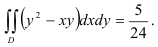
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:

Заказать контрольную работу по высшей математике

Другие похожие примеры возможно вам будут полезны:

Пример решения заказа контрольной работы №80.

Пример решения заказа контрольной работы №81.

Пример решения заказа контрольной работы №90.

Пример решения заказа контрольной работы №92.