Пример решения заказа контрольной работы №78.
Найдите и изобразите область определения функции
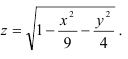
Решение:
Функция
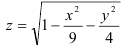
глобально представляет собой корень чётной степени, поэтому область её определения будем находить, учитывая, что подкоренное выражение неотрицательно. Таким образом,
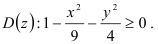
Изобразим область определения функции в прямоугольной декартовой системе координат. Для этого рассмотрим уравнение
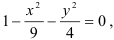
преобразуем его к виду:
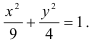
Данное уравнение является каноническим уравнением эллипса. Собственно по каноническому уравнению эллипса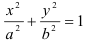 
найдём большую 
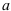и малую 
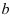полуоси: 
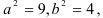откуда 
.
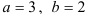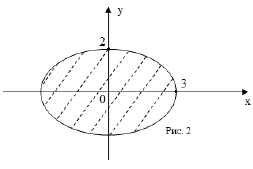
Построим эллипс в прямоугольной декартовой системе координат.
Эллипс разбивает множество точек плоскости на два подмножества: множество точек внутри эллипса и вне его. Определим, какое из них геометрически реализует область определения функции. Для этого возьмём произвольную точку, например, внутри эллипса (0;0) и подставим её координаты в неравенство:
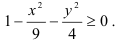
Получим:
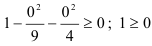
верное неравенство.
Таким образом, (0;0) принадлежит области определения функции, а это означает, что область определения функции
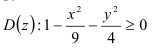
изображается множеством точек координатной плоскости внутри эллипса
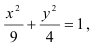
включая точки эллипса (поскольку неравенство
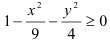
нестрогое) (рис.2).
Ответ: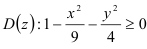 
— множество точек.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №75. |
| Пример решения заказа контрольной работы №77. |
| Пример решения заказа контрольной работы №80. |
| Пример решения заказа контрольной работы №81. |
