Пример решения заказа контрольной работы №6.
Найдите матрицу, обратную матрице

Решение:
1. Находим определитель матрицы 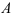 .
.
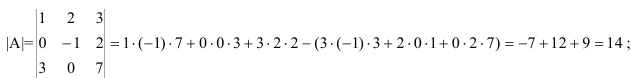
 матрица
матрица 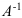 существует.
существует.
- Найдем алгебраические дополнения каждого элемента матрицы
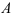 :
:
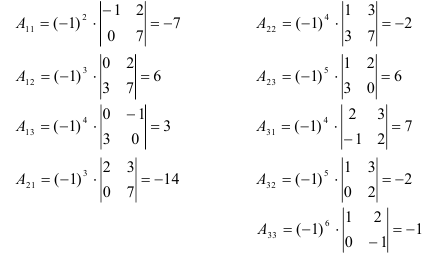
Составляем матрицу из алгебраических дополнений 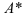 :
:
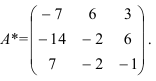
- Транспонируем матрицу
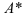 :
:
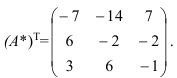
4.Составляем обратную матрицу по формуле:
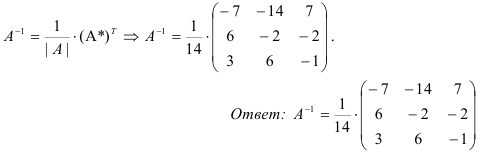
Для нахождения ранга матрицы ее нужно привести к стунен чат ому виду: под первым ненулевым элементом каждой ее строки стоят нули в нижних строках:
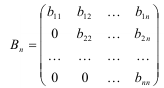
Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк. Ранг матрицы обозначается 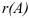 .
.
Приведение матрицы к ступенчатому виду осуществляется с помощью элементарных преобразовании:
• умножение всех элементов строки или столбца матрицы на число, отличное от нуля;
• перестановка местами строк;
• вычеркивание нулевой строки;
• прибавление к элементам некоторой строки соответствующих элементов другой строки, умноженных на любое действительное число.
Если одна матрица получается из другой с помощью элементарных преобразований, то такие матрицы называются же и валентными и обозначаются 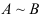 .
.
Для упрощения вычислений на первое место лучше ставить ту строку, в которой первый элемент равен 1.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №3. |
| Пример решения заказа контрольной работы №4. |
| Пример решения заказа контрольной работы №7. |
| Пример решения заказа контрольной работы №9. |

