Пример решения заказа контрольной работы №54.
Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции

Решение:
1. Данная функция определена в том случае, когда знаменатель отличен от нуля: 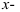
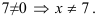
Найдем первую производную функции:
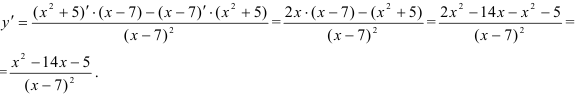
Найдем вторую производную функции:
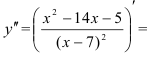
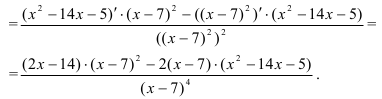
Вынесем в числителе 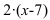 за скобки:
за скобки:
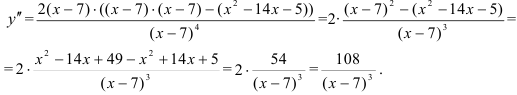
Определим критические точки второго рода: 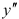 не может быть равна нулю, поскольку числитель дроби
не может быть равна нулю, поскольку числитель дроби 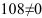 .
.
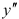 не существует, если
не существует, если 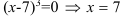 — критическая точка второго рода.
— критическая точка второго рода.
На числовой оси отметим критическую точку 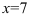 выколотой точкой, поскольку в этой точке функция
выколотой точкой, поскольку в этой точке функция 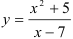 не определена. Эта точка разбивает область определения функции на два интервала
не определена. Эта точка разбивает область определения функции на два интервала 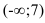 и
и 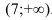 . Расставим знаки второй производной функции
. Расставим знаки второй производной функции 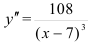 на каждом из полученных интервалов:
на каждом из полученных интервалов:
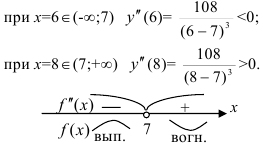
Согласно критерию выпуклости-вогнутости график функции 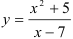 является выпуклым при
является выпуклым при 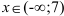 , вогнутым при
, вогнутым при 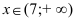 .
.
Точка с абсциссой 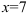 не может быть точкой перегиба, т.к. в этой точке функция не существует (терпит разрыв).
не может быть точкой перегиба, т.к. в этой точке функция не существует (терпит разрыв).
Ответ: график функции 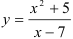 выпуклый при
выпуклый при 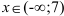 , вогнутый при
, вогнутый при 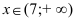 .
.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №50. |
| Пример решения заказа контрольной работы №52. |
| Пример решения заказа контрольной работы №56. |
| Пример решения заказа контрольной работы №58. |

