Пример решения заказа контрольной работы №39.
Найдите производную функции 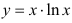 в точке
в точке 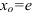 .
.
Решение:
Сначала найдем производную функции 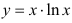 как производную произведения. Воспользуемся правилом
как производную произведения. Воспользуемся правилом 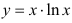 :
:
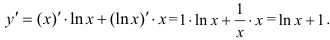
Для нахождения производной функции в точке в производную 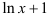 вместо аргумента подставим
вместо аргумента подставим 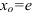 :
:
Тогда
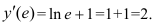
Ответ:
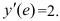
Дифференциалом функции 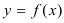 в точке
в точке 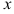 называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 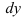 (или
(или 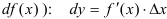 . Поскольку дифференциал независимой переменной равен приращению этой переменной:
. Поскольку дифференциал независимой переменной равен приращению этой переменной: 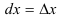 , дифференциал функции равен произведению производной этой
, дифференциал функции равен произведению производной этой
функции на дифференциал независимой переменной: 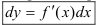 .
.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №36. |
| Пример решения заказа контрольной работы №38. |
| Пример решения заказа контрольной работы №40. |
| Пример решения заказа контрольной работы №42. |

