Пример решения заказа контрольной работы №35.
Найдите точки разрыва функции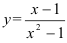 
и определите их род.
Решение:
Функция 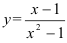является элементарной, следовательно, она непрерывна на области определения.
Найдем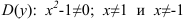 
. Получили, что точки 
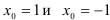являются точками разрыва функции. Для того, чтобы их классифицировать, найдем односторонние пределы функции в указанных точках.
Для точки
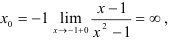
следовательно,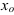 
= -1 — точка разрыва II рода.
Для точки
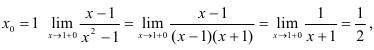
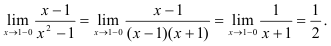
Следовательно, 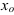= 1 — точка разрыва I рода.
Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то 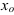= 1- точка устранимого разрыва. Положив 
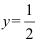при 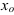= 1, разрыв устранится, функция станет непрерывной.
Ответ: 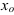=-1 — точка разрыва функции II рода, 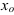= 1 — точка разрыва функции I рода.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №33. |
| Пример решения заказа контрольной работы №34. |
| Пример решения заказа контрольной работы №36. |
| Пример решения заказа контрольной работы №38. |
