Пример решения заказа контрольной работы №34.
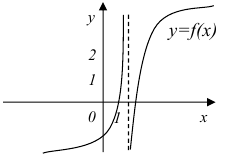
Найдите точки разрыва и определите их род для функции 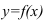 , заданной графически:
, заданной графически:
Решение:
Непрерывность функции 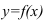 нарушена в единственной точке
нарушена в единственной точке 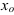 = 1. Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке:
= 1. Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке:
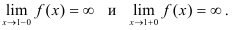
Они существуют, и оба равны бесконечности. Следовательно, точка 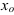 = 1 является точкой разрыва II рода функции.
= 1 является точкой разрыва II рода функции.
Ответ: 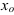 =1 — точка разрыва функции II рода.
=1 — точка разрыва функции II рода.
Если функция задана аналитически, для нахождения и классификации ее точек разрыва удобно использовать следующую технику:
1) выясните, является ли функция элементарной (если да, то она непрерывна на своей области определения);
2) найдите область определения функции и исследуйте на разрыв точки, не принадлежащие ей (но находящиеся внутри области); если перед Вами — функция — скобка, обратите внимание на повторяющуюся в способе задания точку;
3) найдите односторонние пределы функции в каждой из таких точек и в зависимости от этого классифицируйте разрыв (если односторонние пределы существуют и конечны, в точке — разрыв I рода; если хотя бы один из этих пределов не существует или равен бесконечности, в точке -разрыв II рода).
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №31. |
| Пример решения заказа контрольной работы №33. |
| Пример решения заказа контрольной работы №35. |
| Пример решения заказа контрольной работы №36. |

