Оглавление:
Линейные неравенства с двумя переменными
Пример №314.
Найти множество точек координатной плоскости, удовлетворяющих неравенству
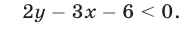
Решение:
Уравнение 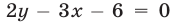 является уравнением прямой (рис. 26.5), проходящей через точки
является уравнением прямой (рис. 26.5), проходящей через точки 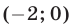 и
и 
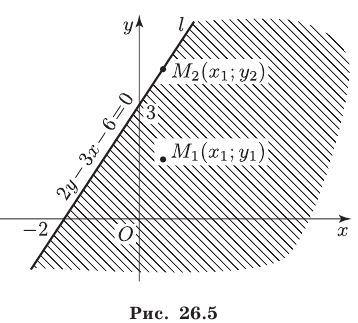
Пусть  — точка, лежащая ниже прямой
— точка, лежащая ниже прямой  (в заштрихованной на рис. 26.5 полуплоскости), а
(в заштрихованной на рис. 26.5 полуплоскости), а 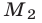 — точка с абсциссой
— точка с абсциссой 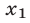 и ординатой
и ординатой 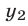 , лежащая на прямой
, лежащая на прямой 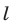 . Тогда
. Тогда
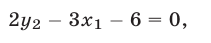
а
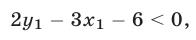
так как 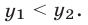
Таким образом, в любой точке 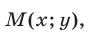 лежащей ниже прямой
лежащей ниже прямой 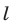 , выполняется неравенство (1). Аналогично, в любой точке
, выполняется неравенство (1). Аналогично, в любой точке 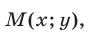 лежащей выше прямой
лежащей выше прямой 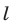 , выполняется неравенство
, выполняется неравенство
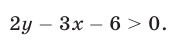
Точно так же можно решить неравенство общего вида
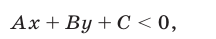
где по крайней мере одно из чисел 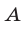 и
и 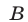 не равно нулю.
не равно нулю.
Если 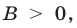 то неравенство (2) выполняется во всех точках, лежащих ниже прямой, заданной уравнением
то неравенство (2) выполняется во всех точках, лежащих ниже прямой, заданной уравнением
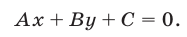
Если 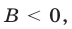 то неравенство (2) справедливо в точках, лежащих выше этой прямой.
то неравенство (2) справедливо в точках, лежащих выше этой прямой.
Если 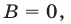 то неравенство (2) примет вид
то неравенство (2) примет вид
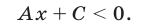
Это неравенство равносильно неравенству 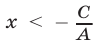 при
при 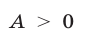 и неравенству
и неравенству 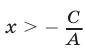 при
при 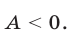
Например, неравенство 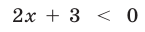 равносильно неравенству
равносильно неравенству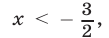 которому удовлетворяют точки, лежащие слева от прямой
которому удовлетворяют точки, лежащие слева от прямой 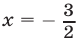 (рис. 26.6).
(рис. 26.6).
В общем случае прямая
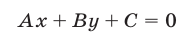
разделяет плоскость на две полуплоскости, в одной из которых выполняется неравенство (2), а в другой — неравенство
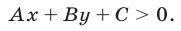
Чтобы решить неравенство (2) или (3), достаточно взять какую-нибудь точку  не лежащую на прямой
не лежащую на прямой 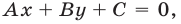 и определить знак числа
и определить знак числа 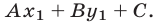 Например, неравенство
Например, неравенство
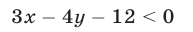
верно в полуплоскости, расположенной выше прямой 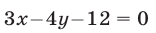 (рис. 26.7), так как при
(рис. 26.7), так как при 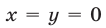 выражение
выражение 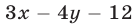 отрицательно. Эта прямая проходит через точки
отрицательно. Эта прямая проходит через точки 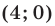 и
и 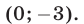
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

