Оглавление:





Пример расчета тонкостенного стержня
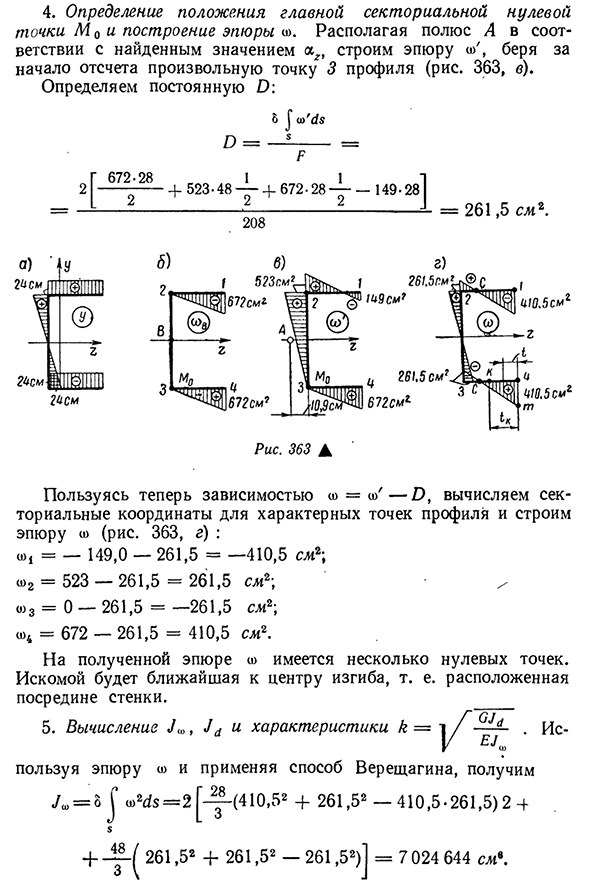
- Пример расчета тонкостенных стержней Постройте график нормальных и касательных напряжений относительно поперечного сечения стержня в уплотнении (рис. 362). 1. Определение центра тяжести сечения. Так как поперечное сечение стержня симметрично относительно оси ОГ(рис. 362, а), положение центра тяжести определяется по одной координате 2-29-2-14, 5 4-46-2-1 2-29-24-46-2 — 2
= = 8,5 см. 2. Расчет главного центра момента инерции. В этом случае для расчета достаточно знать только главный момент инерции, то есть, значение ЛГ. Для его расчета мы используем метод Верещагина, по которому ранее построили график (рис. 363, а): В Уч= 2 1^24 •
28 — 24 • 2 4- ■ — |- 24 • 2 8 2 944 ссылка. 3. Определите положение центра сгиба Людмила Фирмаль
. Чтобы упростить расчет, выберите любые полюса, чтобы участок не распространялся больше всего на профиль. Начальная точка счета площади сектора обозначается пунктом 3. 363, б). Согласно формуле (13.88), мы имеем . Г./ 672-28 / 2 ———— 8\2 Но — ———— = —————— g C82 944 История Это связано с одной из определенных координат
центра изгиба, то есть АС равен нулю. 4-264 определить положение главного вектора нулевой точки M o и построить график o>. Если вы разместите полюс A в соответствии с найденным значением AG, вы создадите график o/и возьмете любую точку 3 профиля в качестве начальной точки(рис. 363, в). Определите константу O: G672-28 Два.[— 1-1 4- 523-48——4- 672-28 — — 149-28 2/2 Двести восемь =261. 5cm2.
- Пять.) 2. система GPS Но) 24см(‘ — По Т11 ) г 24см б) ‘ЦСП§[/φ72σ 1——————► г Mo № д)2 6 1,5 с м^с я 0,5 см — г Четыре. И 410. 5cm2t 2 149см» @ Семь. МО и i261. В Рис, 363А. Вычислите координаты деления характерных точек профиля и участка o, используя здесь зависимость o>=o/ — P (рис. 363, г): о)! = — 149,0-261,5= — 410, 5см2; СМ2 ; см2;см2. (а)есть несколько нулевых точек. SH2=523-261, 5=261, 5yu3=0-2661, 5=-261, 5 o) 4=672-261, 5=410,5 на полученном участке искомый участок расположен ближе всего к центру изгиба, то есть в центре стенки. 5. Расчет<1a и характеристика K=1/. IP- В Если применить метод Верещагина с использованием графика o), L>=&u o) M5= 2 ^ (4 1 0 ,5 2 + 261,52 — 410,5261,5) 2 4-$ + 261,52 4- 261,52 — 261,52)^ = 7 024 644 ссылка. По уравнению 427dalee(13.4) находим 29-23 . \3 46-23.\ Три. /
2+=311CM1. Характеристику к вычисляют, принимая е=2-106 кг / см? А O-8-105CPSM?. В результате мы имеем 1 / 8-105-311 LLLO-1 К-У2-106-7 024 644 0. 002SL1. 6. Дифференциальное уравнение угла закрутки 6 и подготовка уравнения для определения HS, MS и L40. Начальные параметры, неизвестные в этом примере, равны 60 и 0o — используйте граничные условия для их определения: 1) 0x= / =0 И 2) О;=/=О. Применяем общую формулу угла кручения (13.64) и учитываем, что при o=0 он получается для любой части стержня e=
Отчет Ноль. 0++(а) К (МА\К)» И 6’=СЖ Х4 — (1-СП х). (b)подставляя x=I в уравнение (b) и используя второе граничное условие, вы можете увидеть е;Си К1+(1-Си К1)=0,(в) Откуда (г) Найденное значение 9o вводится в уравнение (а), Людмила Фирмаль
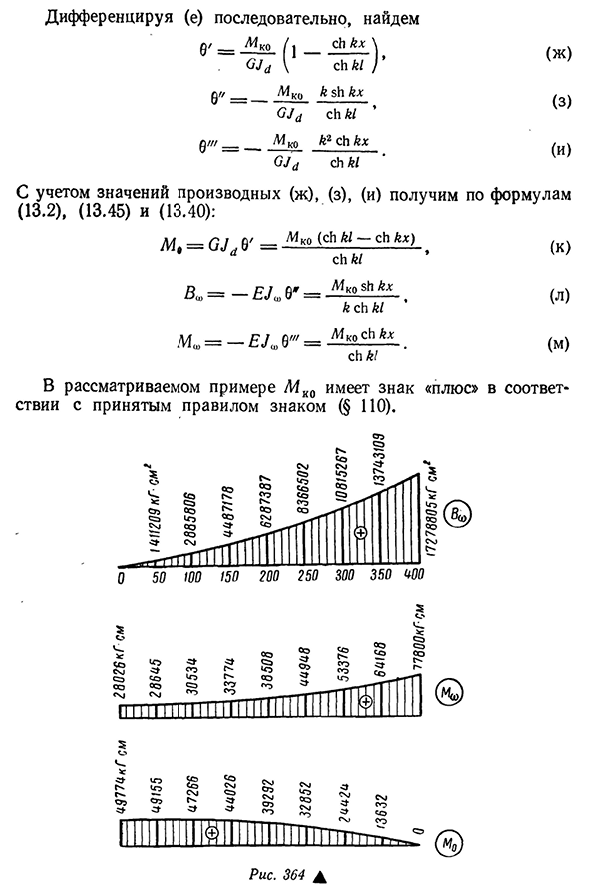
используя первое граничное условие, которое получается после простого преобразования Я-714K0(0 6^\ысь К1 (Д) После выражения (а) подставляем его в(D) и(Е) bidifferential (е) в преемственности, мы находим 9’=714ko L_s к ч\67^ь\Г / ‘ Д//__ _ ОМИН К А К ч (M d XY K1V» ‘ =__M co K2XY K x0 4XY K1 & г) Принимая во внимание значения производных (g), (z), (I), формулы (13.2), (13.45) и(13.40):M9=SP0’= — ^Ko-1^..^—(С)C1W е»= — е С6’=м с»З. ы.**, (л) К Сы К1 Ма= — е. 1.»0″‘=. (м) ы! » В этом примере L4IO имеет знак плюс в соответствии с принятым знаком правила (§110). 5° Смотреть Ex С помощью CM ко o43 Смотри сотни cm03 И см ОО°см о -3 em3- о-см. Да, да, да, да, да, да, да, да. 11ii1111ttttggg^г R есть. 364А Число 429-го M K0 равно L4K0=
2000(28+10,9) = 77 800 кг-см. Из таблицы гиперболических функций * находим C!1к1=ее 0.0042-400=ее 1.68=2.776. Таким образом, мы имеем: L40=77 800 — 28 026 it Kh\VSH=6 672 384zy Kh; M I)=28 026 it Kh. (н) (о)) (п) Согласно формулам (n), (o) и (p), рис. Для удобства таблица предварительно создается, так как построены HSH, m sh и M0 участка 364. 14. требуются числовые данные. Т а б л и Ц А14 Х,см х ж Х Х СК В<О, кг*см2 Л^О) * кг * см м<9кг^см Ноль. Ноль. 0 1,0000 0,000 28026 49774 50 0.21 0.2115 1.0221 1411209 28645 49155 100 0.42 0.4325 1.0895 2885806 30534 47266 150 0.63 0.6725 1.2051 4487178 33774 44026 200 0.84 0.9423 1.3740 6287387 38508 39292 250 1,05 1,2539 1,6038 8366502 44948 32852 300 1,26 1,6209 1,9045 10815267 53376 24424 350 1,47 2,097 2,289 96
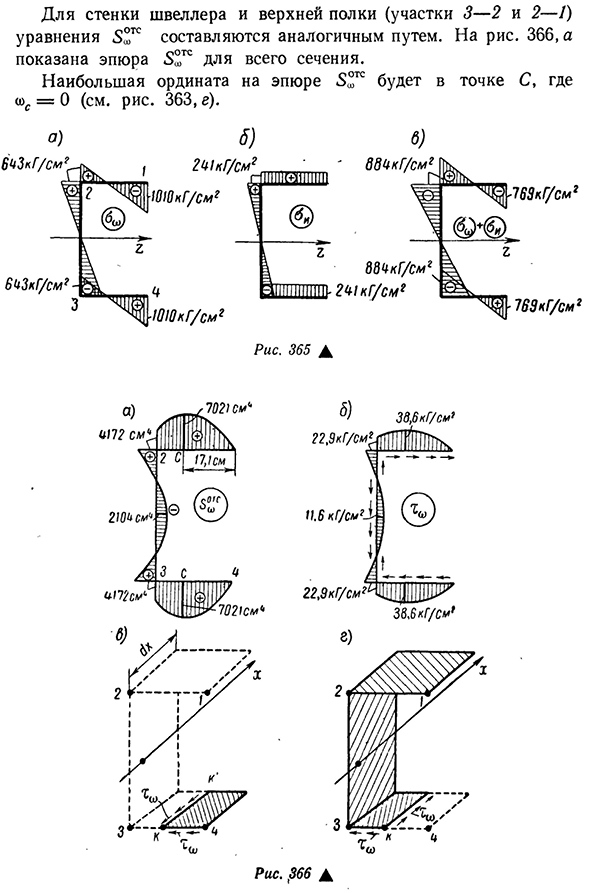
13743109 64168 13632 400 1,68 2,5896 2,760 17278805 77800 0 7. Расчет нормального напряжения. В сечении стержня, помимо нормального напряжения, связанного со сдержанным кручением, существует также напряжение si, связанное с поперечным изгибом стержня относительно оси G. данное сечение Давайте сначала определимся»,. Для этого подставьте число в Формулу (13.47).1ш: 17 278 805 О. P7 = ———— со=2.4597 Инк. (И) 7 024644′ Можно использовать формулу (а). 365, участок будет построен, причем значения разделенных координат взяты из участка co, показанного на рисунке. 363г История * См. Приложение I 430как видно, что признаки участка sh и ash совпадают, плюс соответствует растягивающему напряжению, а минус сжатие является общим признаком деформации сердечника
при сдержанном скручивании. Максимальное значение напряжения zi в крайних волокнах полки определяется по известной формуле ± Юта±2000-400 82 944 * 25=±241 км!см* Для риса. 365, b представляет фигуру напряжения бзкг / см*- K2EC и 3 Шесть.) 24 / КГ / СМГ.////1I1/ВТ||/ Два. Шесть.) GCS / S^ м н и 769кг / СМГ Рис 365А Рис 366А 432 численно это вертикальное седло можно определить как площадь треугольника 4TC. Следует помнить, что формула (а) определяет напряжение сдвига в продольном сечении отрезной части стержня. Есть обход профиля, эти напряжения. 366, в) плоскость отсечной части элемента к-К1 (1х (заштрихована на рисунке). В противоположном направлении, то есть от точки 1 к точке 2, а затем
к точкам 3 и 4, участок 5°TC имеет знак, противоположный знаку, показанному на рисунке. 366, а. напряжение TJ в этом случае показано на рисунке. 366 г, который также затенен отрезной частью. Направление тангенциального давления в поперечном сечении стержня задается эквивалентным законом. Как использовать 366, b и d, их направление в точке K остается одинаковым в обоих вариантах обхода. Для риса. 366, б показывает участок и его направление в поперечном сечении стержня. Какова величина тангенциального напряжения?< «, Как видно из графика, невелика по сравнению с численным значением нормального напряжения в данном случае. Тангенциальное напряжение, связанное с боковым изгибом, также невелико. Самые крупные из них происходят на нейтральной оси выхлопного газа(см.. 362,6) раздел, будет <25^ = 2000(29.2.24+ 23.2.11,5) = .
Смотрите также:

