Оглавление:




Пример расчета неразрезной балки
- Пример расчета непрерывной балки Вы также можете выбрать следующие параметры: 5.32 и= 6, /2 = 10, 13 = 4, /4 = 8 m; s=2m;=3, P2=2TS; q=0,6 TS/m; p-1,2; L? =2100 кгс / см2. Решение. Балка в три раза статичнее неопределенной (три промежуточных опоры). Для всех промежуточных опор мы ввели шарниры и применяем неизвестное время опоры. Таким образом, вместо заданной статической
неопределенной балки рассмотрим четыре простые балки, лежащие на шарнирной опоре, и запишем три мгновенных уравнения для каждой опоры двух соседних пролетов, за исключением нагрузки в пролете. Имея в виду, что MA=L14=0, получим систему из
трех уравнений; 32/I, 4-10L42= — lOAlj+28l4a4-4M,=-6/?; 4l4a4-24L43= -. Людмила Фирмаль
Построить график изгибающего момента M°и поперечной силы Q°для каждого пролета. 5.32, в, д). Определите правильную часть уравнения для трех моментов. Согласно таблице. 5.10 поиск / ?=В* + 4 = ( / 2 — 4 — = — u-5 130/? =S+4= — § — =25; 4=СФ-+4= — ^л(z4_C)=J2 на. Подставляя полученные данные в уравнения трех моментов, решаем систему уравнений: 16Mf+5L12==-91;5L11+IL12+2L13=-75; Мг+6Л43=-18. Чтобы решить эту систему, мы применяем вышеуказанную технологию.
В нашем случае:= — 6flf= — 6= = −182; С2= — = −6. 25= = −150; С3=-67$=-6. 12= = −72. Тогда примите −1 зет 2(т+1и- 1=19,9. Определите L43 по формуле (d)) 5.32 невмешательства S1ZH1 4-AA и 2 для 4-z и 1za2 4-2 (/3Z4) И. 1134.8 464.8 =-2,441 темы. Подставляя L13 в третье уравнение системы уравнений трех моментов, получаем TEM из L42==-3351,
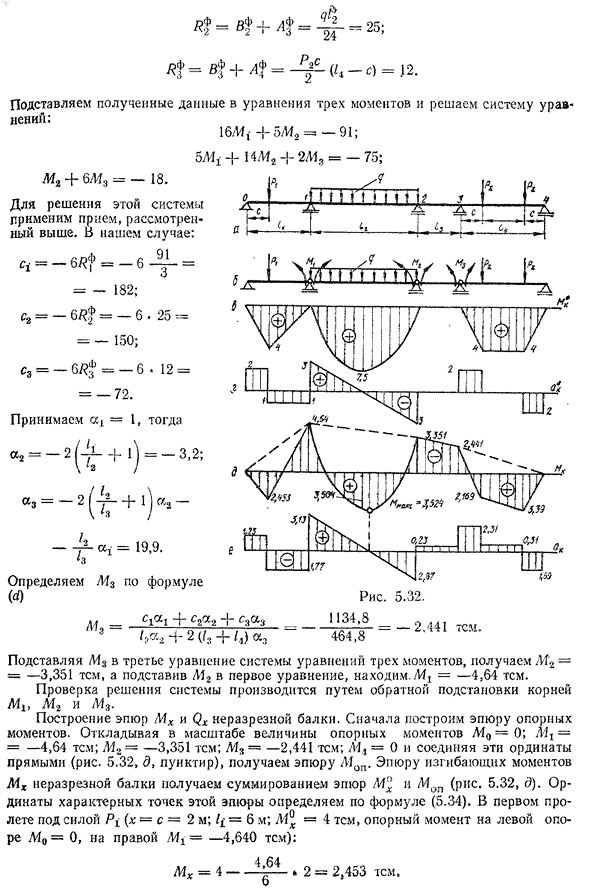
- и находим, подставляя m2 в первое уравнение. L1T=-4,64 ТЕМ. Проверка решения системы осуществляется путем обратной подстановки корней M lt M2 и L13. Непрерывный луч MX и Q. построение t во-первых, давайте построим момент для поддержки. Отложите масштаб величины опорного момента L40= = 0; 41! = = −4,64 тема; L12=-3,351 тема; M3=-2441 тема; L44 = 0 и линейный (рис. 5.32, d, пунктирная линия), мы получаем график Mos. График изгибающего
момента M x непрерывной балки получается суммированием графика m°и L40P(рис. 5.32, г). Координаты характерных точек этого участка определяются по формуле (5.34). В первом пролете под действием силы Pi (x=C = 2m;/4=6m; L4°=4TEM, левая опора L40 = 0 опорный момент, правая L14=-4,640 TEM): 4 64 МХ= 4 ——-4 —. 2=2,453 темы. 131″3,351_4,64″ в середине второго пролета » MH= 7,5 ——- Джо.— • 5 ——- Джо — » 5=3,504 темы. В четвертом полете под действием силы Р2Л4Ж= 4 ———- z — — — — — — — =2,169 темы} Отчет 2 441•2 м х= 4— ■■■’■ 1 ~ ■■ = 3,39 те самые. Найти максимальный изгибающий момент во втором пролете. Для этого запишите формулу изгибающего момента этого пролета qx2-2 M2Ga-х )
К Или, заменив данные, о которых идет речь, MX= — O. Zx2 4-3, 13 L:-4,64, Людмила Фирмаль
дифференцирует это выражение на x и уравнивает его до нуля:-0, 6×0+3,13=0. Итак, абсцисса сечения, соответствующего экстремальному моменту, равна、 3.13 х o= — СКР— ’ 5,2 2М — Подставляя x0 в выражение момента, получаем L4max=-0,3•5,22 a+ 3,13 «5,22-4,64 = 3,524». Вертикальная ось графика поперечной силы определяется выражением(5.35). Участок Q°уже создан. Чтобы построить график QX непрерывной балки, вычислите боковые силы, вызванные действием опорного момента: Для первого полета 0,77 ТС; Второй И aq3 −3’3 5 1.+4^=0,1 3ТС; 10 Для третьего — 2,441 4- 3,351 Четыре. И aq3 И для четвертого Aq4 суммы 2,441 n t,™ — 8 —
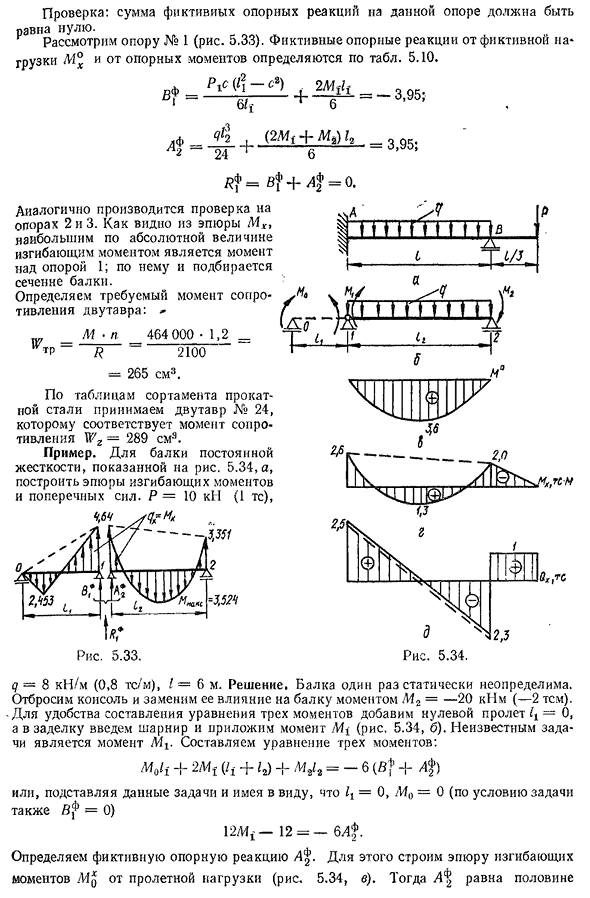
=0,31 TS, добавляем AQ к участку Q°, получаем участок Qx(рис. 5.32, е). Эталонная реакция данного непрерывного пучка определяется по формуле (5.33). Если построить график Qx, то их можно также определить по»скачку» графика Qx на линейной опоре: Rn=Q — Qn>где Q» и-участок 3=2,31-0,23=2,08 ТС;/?4=1,69 Ц. 132 проверка: общее количество фиктивных ссылочных ответов на эту поддержку должно быть равно нулю. Опора № 1 (Рис. 5.33). Фиктивная нагрузка М°и фиктивные опорные реакции от опорного момента определяются по таблице. 5.10 На 2Mt lt’ = —— 6^——- + — g — — — 3. 9 5, ф З Л (2Mf+мг) 2 — 24 + 6 д’Андреа 9 5. 4=ВФ+ДФ = о. Производится проверка
Диалогически на опоре 2из. Как видно из графика MX, максимальным абсолютным значением изгибающего момента является момент опоры 1. Определите необходимый момент сопротивления двутавровой балки: «M■p464 000-1, 2 ^Tr—2 1 0 0 =265см3. Согласно таблице в ассортименте проката стального, у нас двутавровой балки нет. Принимаем 24, это соответствует моменту сопротивления-289 см3. Например. Для неподвижных и жестких балок. 5.34, построена диаграмма изгибающего момента и силы сдвига. Р=10кн(1ТС), Рис 5.33. Рис. 5.34 よ 9=8кн/м(0,8 ТС / м), I=6 м. пучок один раз статически неопределим. «Я думаю, что это будет отличная игра», — сказал он.2
= — 20kNm (- 2TEM) момент для замены. Для удобства вычерчивания формулы трех моментов добавим нулевой пролет-0,а в уплотнение введем шарниры и приложим момент m±.5.34, б). Неизвестный момент, о котором идет речь, — L4t. Molt+2Mt(Zf+Z2)+L4a/a=-6 (Bf+4) или, заменяя данные задачи, 0, L40=0(Также=0 в зависимости от условия задачи) 12L4^-12= — 6А. Мы определяем гипотетическую эталонную реакцию a^. Для этого постройте график изгибающего момента пролетной нагрузки (рис. 5.34, в). Тогда ох! Равный половине§ 133T а б л и Ц А5. 11. Изгибающий момент, боковая сила и реакция опоры от рабочей нагрузки в балке с равным расстоянием
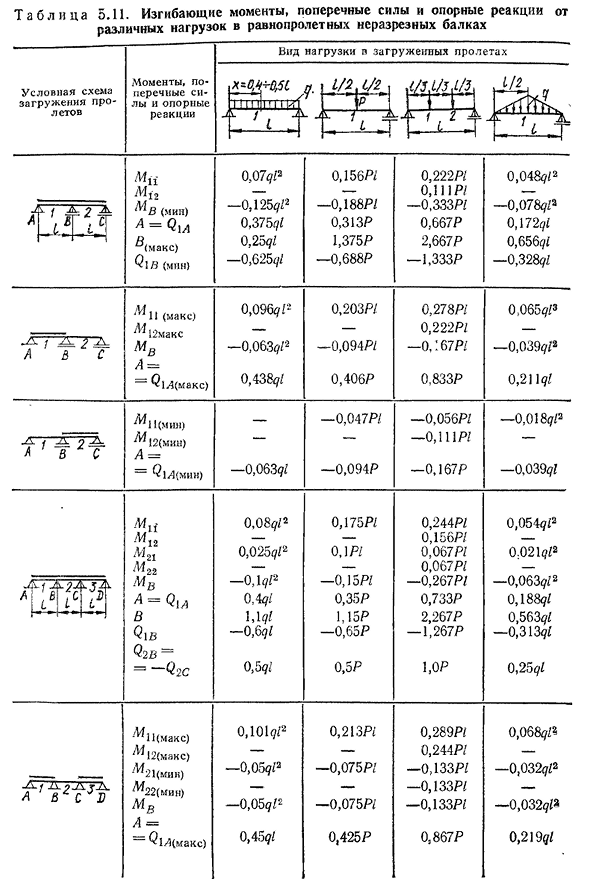
Как работает загрузка пролета Моменты, боковые силы и опорные реакции S нагрузка тип нагрузки пролет М12 A1d (min) A=Q1A Р°(максимум) Q1B(мин) 0.07 Qп −0.1259? 0.375^ 0,25 ГЗ-0,6252/2 −0,033®: 4= ‘ 3,6•6=7,2,2. В Формуле для 4 замененных трех моментов находим Al= — 26kNm опорный момент, положенный под левую-2,6 те, под правую-2 те линии (на рис. 5.34, g, пунктирная линия), получаем график опорного момента. Теперь»наложите» параболу, м°на участок между опорными моментами и завершите участок в консоли. Это будет окончательный график изгибающего момента ТМ(рис. 5.34, г). Чтобы получить график поперечных сил, добавьте график Q»от нагрузок пролета и моментов опоры(рис. 5.34, д) (-2.6 темы). Соединение от-И
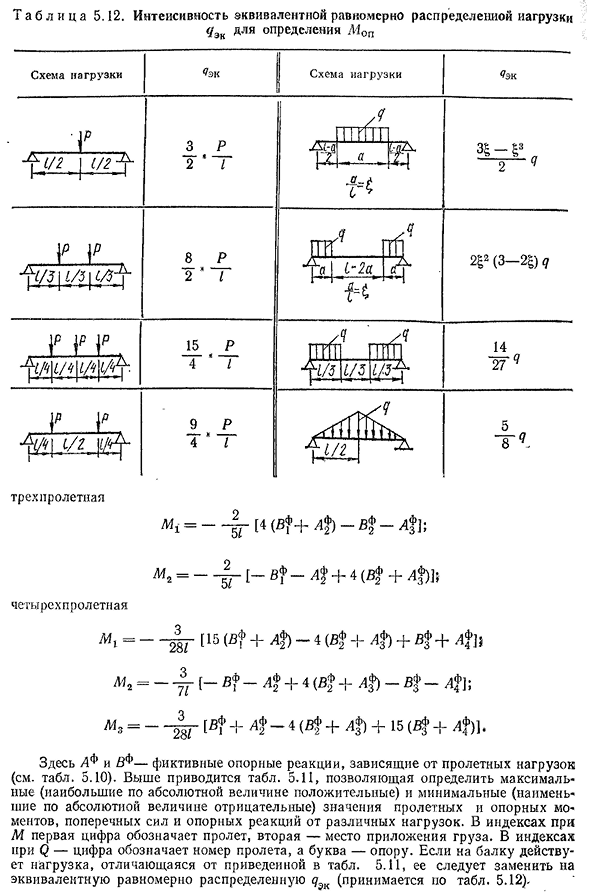
И эти 5: 35 рис. АQ=—- 2 ‘°Б+2 ‘ 6=0.1 ТС;Ц=Г°+ах. Равный пролет непрерывной балки. В частном случае/x=12= / 3= / 4=i и EJ-const по всей длине балки(рис. 5.35), формула момента опоры при любой нагрузке выглядит следующим образом: две закрученные балки М1=—| — (Б-В * ) ; 135T ably CA5. 12. Интенсивность равномерно распределенной нагрузки q3K эквивалентна определению L10p Трехпролетный Ми= — И(4+4)-В* — Л]; Я=—А-[- В-А * +4(Б+Л Ф)]} Fourspan /а= — ~г[15(Б + 4 -4 (4 + 4 ) + 4 + 41> L42= — а[тюнинг F_L F_1_4(в F_1_L Ф) тюнинг F_L| ]; L43= — [в? +4_4 (V F+L F) 15 (V F+L F) B Где A*и YF-гипотетические ответы
поддержки в зависимости от нагрузки на пролет(см. таблицу). 5.10). Выше находится таблица. Когда пядь и поддержка от различных нагрузок, поперечных усилий и реакции поддержки максимальное (самое высокое абсолютное значение положительное) и минимальное (самое низкое абсолютное значение отрицательное) значение индекса м, первое ссылаются на пядь и второе ссылаются на место применения нагрузки. Q-значный индекс указывает на количество пролетов и поддержку символов. Если нагрузка, действующая на балку, отличается от приведенной в таблице. 5.11, он должен быть заменен равным распределенным равномерно<?ЕС (принято в соответствии с таблицей. 5.12).
Смотрите также:
| Полный расчет балок на прочность | Изгиб круглых пластинок, нагруженных симметрично относительно центра |
| Концентрация напряжений при изгибе | Изгиб равномерно нагруженной круглой пластинки |

