Пример №76.3.
Определить радиус сходимости ряда
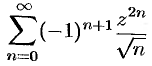
и исследовать сходимость ряда в точках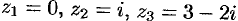 
.
Решение:
Воспользуемся признаком Даламбера. Здесь
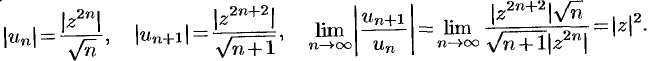
Ряд сходится при всех 
, удовлетворяющих неравенству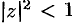 
, т. е.
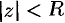. Кругом сходимости является круг с центром в точке 
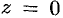и радиусом 1.
Точка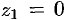 
лежит внутри круга сходимости, в этой точке ряд сходится абсолютно. Точка 
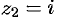лежит на границе круга сходимости, в этой точке ряд может сходиться (абсолютно или условно) и расходиться. Подставляя значение 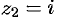в выражение общего члена ряда, получим 
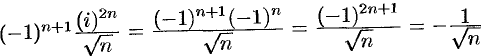. Числовой ряд с общим членом 
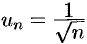расходится согласно интегральному признаку Коши (теорема 60.5). Следовательно, в точке 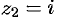степенной ряд 
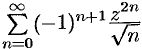расходится.
Точка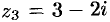 
лежит вне круга сходимости, ряд в этой точке расходится.
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:
