Пример №63.2.
Найти область сходимости ряда
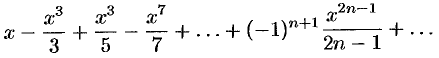
Решение:
Заданный рад неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем:
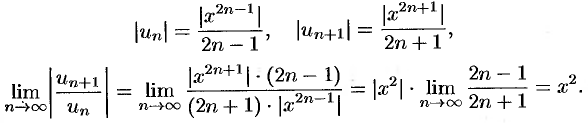
Ряд абсолютно сходится, если 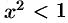 или
или 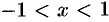 . Исследуем поведение ряда на концах интервала сходимости.
. Исследуем поведение ряда на концах интервала сходимости.
При 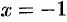 имеем ряд
имеем ряд 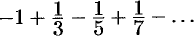 , который сходится по признаку Лейбница.
, который сходится по признаку Лейбница.
При 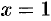 имеем ряд
имеем ряд 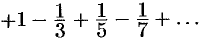 — это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок [—1; 1].
— это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок [—1; 1].
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:

