Пример №62.2.
Исследовать сходимость функционального ряда
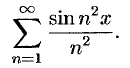
Решение:
Составим ряд из абсолютных величин членов исходного ряда:
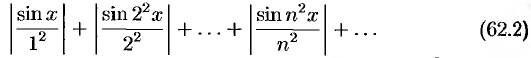
Так как при любом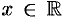 
имеет место соотношение 
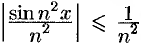, а ряд с общим членом 
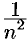сходится (обобщенный гармонический ряд, 
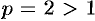, см. п. 60.4), то по признаку сравнения ряд (62.2) сходится при 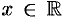. Следовательно, исходный ряд абсолютно сходится при всех 
.
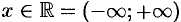Среди функциональных рядов в математике и ее приложениях особую роль играет ряд, членами которого являются степенные функции аргумента 
, т. е. так называемый степенной ряд:
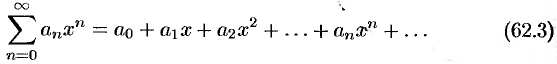
Действительные (или комплексные) числа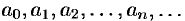 
называются коэффициентами ряда (62.3), 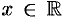— действительная переменная.
Ряд (62.3) расположен по степеням . Рассматривают также степенной ряд, расположенный по степеням (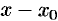
), т. е. ряд вида
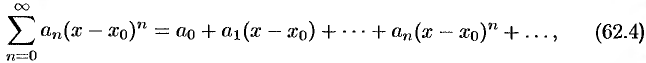
где 
— некоторое постоянное число.
Ряд (62.4) легко приводится к виду (62.3), если положить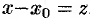 
. Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (62.3).
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:
