Пример №59.3.
Исследовать сходимость ряда
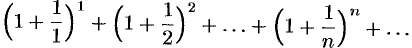
Решение:
Данный ряд расходится, т. к.
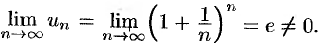
Теорема 59.1 дает необходимое условие сходимости ряда, но не достаточное: из условия 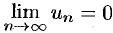 не следует, что ряд сходится. Это означает, что существуют расходящиеся ряды, для которых
не следует, что ряд сходится. Это означает, что существуют расходящиеся ряды, для которых 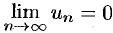 .
.
В качестве примера рассмотрим так называемый гармонический ряд
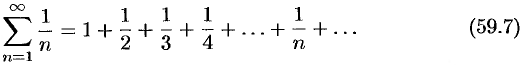
Очевидно, что 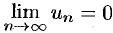 . Однако ряд (59.7) расходится. Покажем это.
. Однако ряд (59.7) расходится. Покажем это.
Как известно (см. (17.14)), 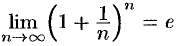 . Отсюда следует, что при любом
. Отсюда следует, что при любом 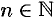 имеет место неравенство
имеет место неравенство 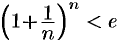 . Логарифмируя это неравенство по основанию
. Логарифмируя это неравенство по основанию 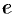 , получим:
, получим:
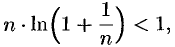
т.е.
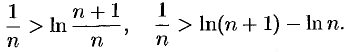
Подставляя в полученное неравенство поочередно  получим:
получим:
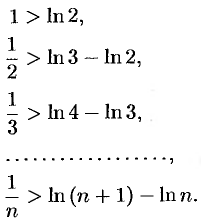
Сложив почленно эти неравенства, получим 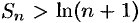 . Поскольку
. Поскольку 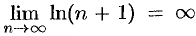 , получаем
, получаем 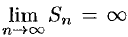 , т. е. гармонический ряд (59.7) расходится.
, т. е. гармонический ряд (59.7) расходится.
В качестве второго примера можно взять ряд
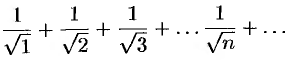
Здесь 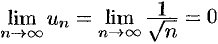 . Однако этот ряд расходится.
. Однако этот ряд расходится.
Действительно,
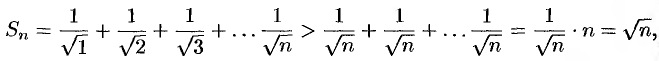
т.е. 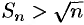 . Следовательно,
. Следовательно, 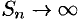 при
при 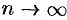 , ряд расходится.
, ряд расходится.
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:

