Пример №49.3.
Найти частное решение уравнения
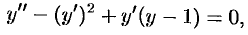
удовлетворяющее начальным условиям: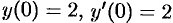 
.
Решение:
Уравнение имеет вид (49.10). Положив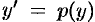 
, 
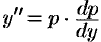получаем:
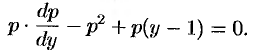
Так как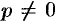 
(иначе 
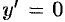, что противоречит начальному условию 
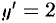), то 
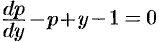— получили линейное ДУ первого порядка.
Проведем решение полученного линейного ДУ методом Бернулли (п. 48.4). Полагаем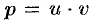 
. Имеем: 
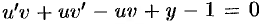, или 
.
Подберем функцию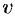 
так, чтобы 
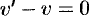. Тогда 
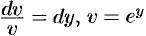. Получаем:
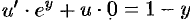, т. е. 
.
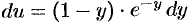Интегрируя это равенство, находим, что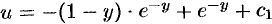 
. Следовательно,
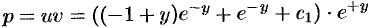, или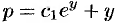 
.
Заменяя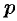 
на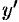 
, получаем: 
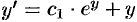. Подставляя 
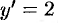и 
это равенство, находим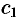 
:
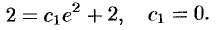
Имеем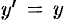 
. Отсюда 
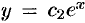. Находим 
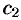из начальных условий: 
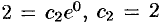. Таким образом, 
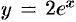— частное решение данного ДУ.
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:
