Пример №49.2.
Решить уравнение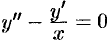 
.
Решение:
Полагаем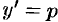 
, где 
, 
.
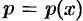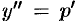Тогда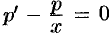 
. Это уравнение с разделяющимися переменными: 
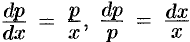. Интегрируя, получим 
, 
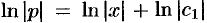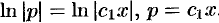. Возвращаясь к исходной переменной, получим 
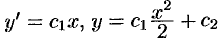— общее решение уравнения.
III. Рассмотрим уравнение
которое не содержит явно независимой переменной 
.
Для понижения порядка уравнения введем новую функцию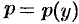 
, зависящую от переменной 
, полагая 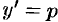. Дифференцируем это равенство по , учитывая, что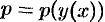 
:
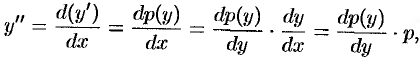
т. e.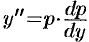 
. Теперь уравнение (49.10) запишется в виде 
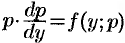. Пусть 
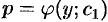является общим решением этого ДУ первого порядка. Заменяя функцию 
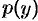на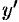 
, получаем 
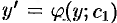— ДУ с разделяющимися переменными. Интегрируя его, находим общий интеграл уравнения (49.10):
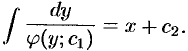
Частным случаем уравнения (49.10) является ДУ
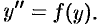
Такое уравнение решается при помощи аналогичной подстановки: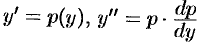 
.
Так же поступаем при решении уравнения 
. Его порядок можно понизить на единицу, положив 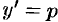, где 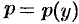. По правилу дифференцирования сложной функции находим 
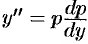. Затем найдем 
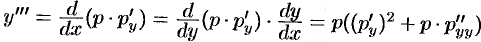и т. д.
Замечание. Уравнение (49.8) также можно решать, применяя подстановку 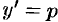, где .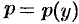
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:
