Пример №25.11.
Из шара радиуса 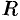 выточить цилиндр наибольшего объема. Каковы его размеры?
выточить цилиндр наибольшего объема. Каковы его размеры?
Решение:
Обозначим через  и
и  высоту и диаметр цилиндра. Тогда, как видно из рисунка 153,
высоту и диаметр цилиндра. Тогда, как видно из рисунка 153, 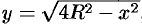 , а потому объем цилиндра
, а потому объем цилиндра
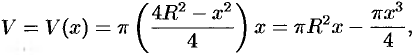
где 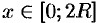 .
.
Находим наибольшее значение функции 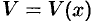 на промежутке
на промежутке 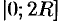 . Так как
. Так как 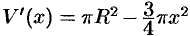 , то
, то 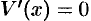 при
при 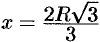 кроме того,
кроме того, 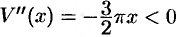 . Поэтому
. Поэтому 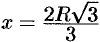 — точка максимума. Так как функция имеет одну критическую точку, то цилиндр будет иметь наибольший объем (равный
— точка максимума. Так как функция имеет одну критическую точку, то цилиндр будет иметь наибольший объем (равный 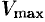 ) при
) при 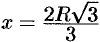 диаметр основания цилиндра равен
диаметр основания цилиндра равен
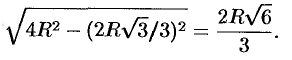
Таким образом, искомый цилиндр имеет высоту, равную 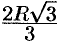 и диаметр, равный
и диаметр, равный 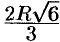 .
.
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:

