Пример №21.
Любую ЗЛП можно привести к каноническому виду. Доказывать теоремы двойственности удобно, когда одна из пары двойственных задач записана в канонической форме. Построим двойственную ей задачу.
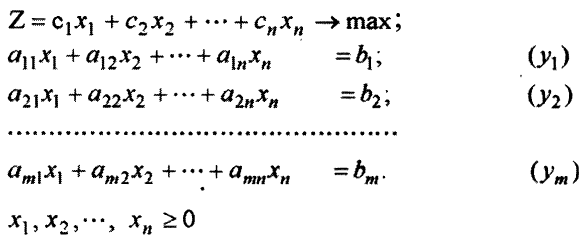
Двойственная задача:
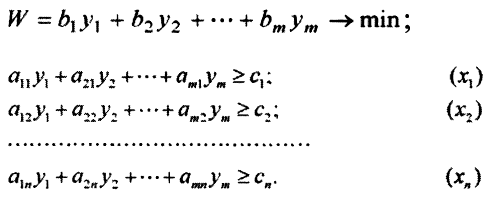
На переменные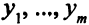 
не наложены условия неотрицательности, так как все ограничения задачи (5.1) — это ограничения-равенства.
Математические модели (5.1) — (5.2) можно записать компактно. Пусть
(
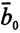— вектор-столбец, записанный как строка);
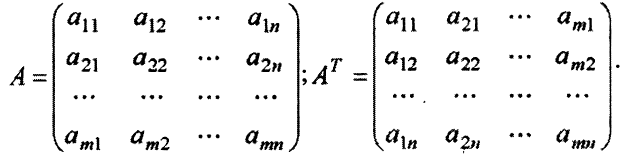
Тогда пара двойственных задач запишется так
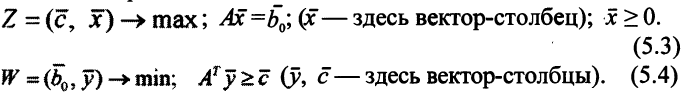
Задача (5.3) — это задача (1); задача (5.4) — задача (2);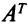 
— транспонированная матрица 
.
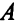Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №19. Решить симплекс-методом |
| Пример №20. Построить задачу, двойственную следующей ЗЛП |
| Пример №23. В табл. 5.1 показано оптимальное решение следующей ЗЛП |
| Пример №24. Рассмотрим такую ЗЛП |
