Пример №19.2.
Исследовать на непрерывность функцию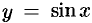 
.
Решение:
Функция 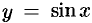определена при всех 
.
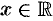Возьмем произвольную точку 
и найдем приращение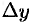 
:
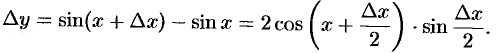
Тогда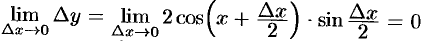 
, так как произведение ограниченной функции и б.м.ф. есть б.м.ф.
Согласно определению (19.3), функция 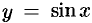непрерывна в точке .
Аналогично доказывается, что функция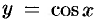 
также непрерывна.
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:
