Пример №16.
Решить ЗЛП
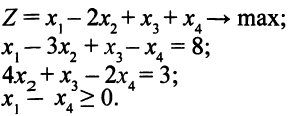
В этом примере базисная переменная есть только у первого уравнения. Введем во второе уравнение искусственную базисную переменную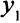 
и решим следующую ЗЛП
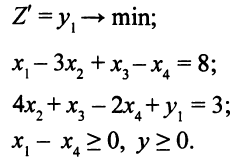
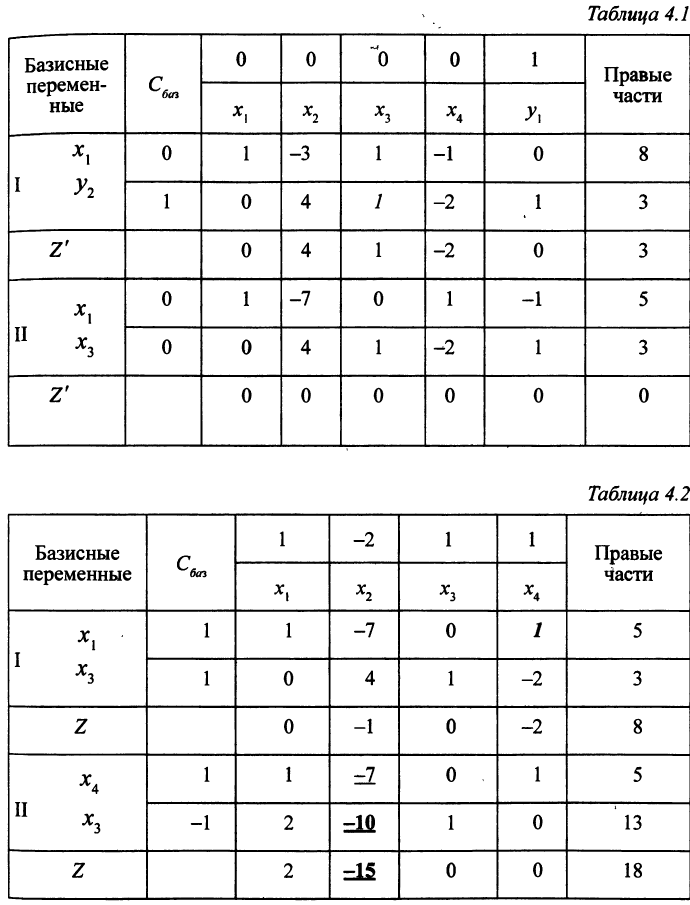
Решение задачи приведено в табл. 4.1. Чтобы уменьшить целевую функцию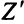 
, нужно сделать базисной переменную 
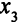с положительной оценкой 
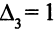. Так как 
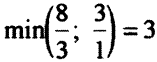, то базисная переменная заменяется во втором уравнении. Искусственная переменная 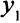становится свободной.
В части II табл. 4.1 записана система уравнений
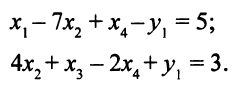
Если отбросить столбец с переменной 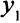, в таблице останется исходная система уравнений, приведенная к стандартному виду
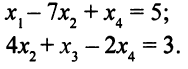
Теперь можно решить исходную ЗЛП (табл. 4.2). Конечно, исходная система уравнений настолько проста, что исключить переменную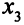 
из первого уравнения и так не составляло никакого труда. Но мы разбираем элементарный учебный пример.
Теперь видно, что целевая функция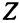 
не ограничена сверху в допустимой области, 
.
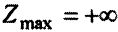Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
