Оглавление:



Применения предельных теорем
- Применение предельной теоремы Теоремы ограничения Пуассона и Мауэрвиля-Лапласа используются для аппроксимации вероятностей Бернулли P {[i = m) и P {10 | <| a </ 2}. Приближение, данное теоремой Пуассона при больших n, называется пуассоновским.
- Теорема Мура-Лапласа, аппроксимация, аппроксимированная канавкой » 1 ~ — Для функции. -e «- плотность нормального распределения (см. §31). T но Распределение Пуассона m ^ -0 «и интеграл * Болезнь φ ^, (*) = ! J в «2 дю, (25)
Существует таблица, называемая интегралом Лапласа. Людмила Фирмаль
- Например, предположим, что вам нужно вычислить вероятность схемы Бернулли с n независимыми тестами и вероятностью успеха p. Рассчитать м | -пр м2-пр „ X, n = -, -: ■, X, n = -y— и положить Ypp Yprya P {/ u, <| Δ <ω2} 2 2 dx = Φ0 (xm;) — Φ0 (xM |). (26) Это допускает некоторые ошибки. Эту ошибку можно оценить, но точные оценки очень сложны, а простые оценки слишком грубые.
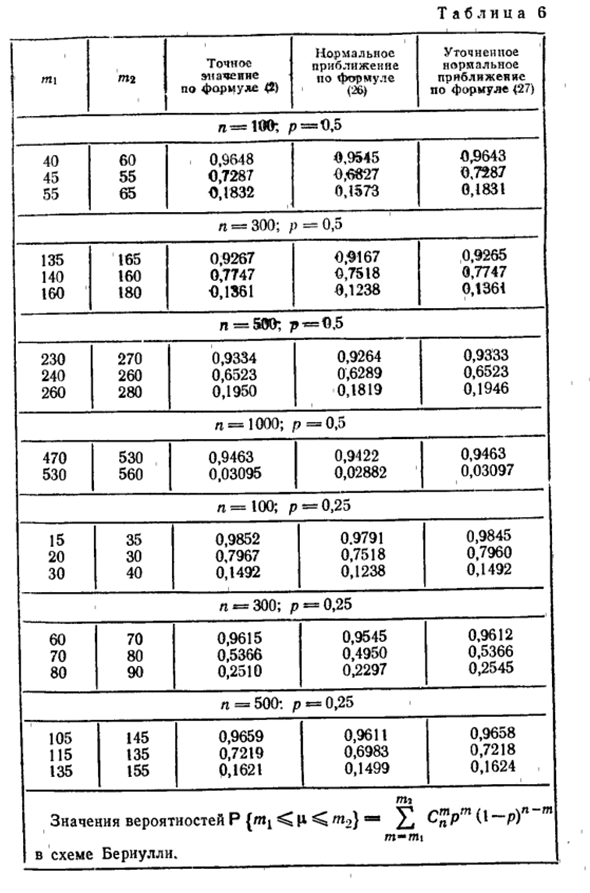
В правой части приближенного уравнения, если настройка слегка изменяет предел интегрирования, эта ошибка значительно уменьшается. P {™ i ~ (27) _ м2 -f 1/2-pr • wi_ * -1 / 2- «» рип Со стола. 6 Можно видеть, что приближенное выражение (27) дает значение вероятности P {rm ^^ p ^ n} с точностью от 3 до 4 цифр после десятичной точки, даже для n из нескольких сотен цифр.
Обычно используемое уравнение (26) не обеспечивает такой точности. Людмила Фирмаль
Смотрите также:
Предмет теория вероятностей и математическая статистика
| Локальная предельная теорема Муавра-Лапласа | Марковская зависимость испытаний |
| Интегральная предельная теорема Муавра-Лапласа | Переходные вероятности |

