Оглавление:







Применение уравнений сохранения для решения задач об установившихся течениях
- Для постановки гидродинамической задачи в случае постоянной плотности используют уравнение неразрывности [(1-a)-(1-c) 1, сингения [(P-d) — (11); (W-d)- (Ш-е); (1U-d)-(1U-e)], линейные и граничные условия. Исходя из этих 2, то распределение давления и скорости.
Для формулировки задачи, влияющей на изотермический поток, который, наряду с начальными условиями и граничными условиями, изменяет плотность и вязкость, можно использовать следующие уравнения: 1) непрерывное уравнение движения [1 (1-а)-(1-с) 1; 2) уравнение движения [(П-А)-(П-С); ((Ш-А)-(Ш-в); (1У-а)-(1У-а)] и формулу компонента Т [(1-а-а)-(3) — п-п (p); 4) уравнение вязкости P = C (P).Из этих 4 соотношений получаем распределение скорости, давления, плотности и вязкости рассматриваемого случая.
Как следствие этого, как только появляются разности температур внутри поля, возникают подъемные силы и эти силы вызывают свободную конвекцию, которая влияет на перенос тела. Людмила Фирмаль
В этом разделе показано, как сформулировать задачу вязкого течения путем упрощения приведенных выше уравнений.Это делается путем удаления члена общей формулы, который в данной ситуации равен (или близок к нулю) нулю.При выборе того, какие элементы исключить, это зависит от интуитивного представления о работе системы (структура потока, распределение давления и т.д.).1. одним из преимуществ этой процедуры является то, что полный список автоматически создается в конце предположения»процесс удаления члена».Мы покажем вам, как это сделать, решив 2 вопроса в главе 2.In в дальнейшем значение этого метода будет объяснено в процессе решения еще нескольких сложных примеров.
В случае осевого течения несжимаемой жидкости в кольцевой трубе сечения 2.3 был составлен баланс импульса, и путем его решения было определено распределение скоростей.Давайте посмотрим, как тот же результат можно получить, упростив уравнение сохранения.Для приведенной выше задачи очевидно, что наиболее подходящими являются цилиндрические координаты.Подумайте о длинной трубе снова и установите z и v в ноль.
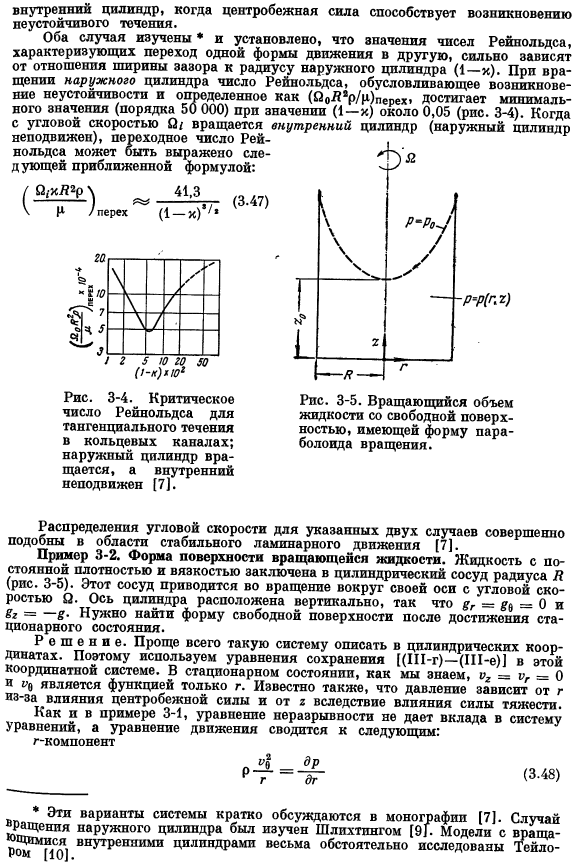
- Оставшаяся составляющая скорости 2₂ в результате цилиндрической симметрии не зависит от 0. Уравнения движения, проецируемые на ось z константами p и p (W-e) , можно описать следующим образом: (3.34 )) Эта формула может быть дополнительно упрощена с помощью непрерывных уравнений.Уравнение неразрывности, в данном случае уравнение (3.35 )) Очевидно, что так.Равное нулю, уравнение (3.34) Это будет выражение О-Л — + ‘7 4Г’ применение двойного интегрирования и граничных условий на g условие, что V является конечной величиной, если R = H равно vii = 0 и если r = 0 равно: Полученные результаты точно соответствуют формуле (2.43).
Из уравнения (P-c), описанного в Примере 2-1, видно, что для пленки жидкости с изменяющейся вязкостью, для стационарного состояния(и игнорирования конечного эффекта) (см. стр. 90).) Затем p.замените 90 выражением. Вводя уравнение (2.23), получаем: [Ссылка уравнения(Уэ)、 (3.40 утра)) Последнее отношение может быть интегрировано с граничным условием= 0, если x = 6.если yo^ x равно 0, то вы получите результат из них, выражение (2.25).
Безразмерные (параметры теплообмена такие как критерий Нуссельта или Стантона, являются функциями критерия Рейнольдса, критерия Прандтля, а при высоких скоростях— функциями параметра Е при условии, что скорости и температуры вдоль границ подобны. Людмила Фирмаль
Используя эти методы, можно сформулировать довольно много других задач.Вот некоторые дополнительные примеры для решения стационарной задачи: некоторые проблемы неустойчивого течения решаются в главе 4.Все более строгие решения доступны в широко популярных книгах[4, 7]. Пример Z-канала.Необходимость Вой 3-3).Вы также можете использовать его в качестве ярлыка для вашего desktop.To ноль.Наклон-это уравнение [(1-6), с. 86), равное нулю, принимает вид: г-compopeit (3-41) 0 =-^-+ РД Текущая(У1-а)-(У1-ж) Можно получить распределение напряжения сдвига t и (g).
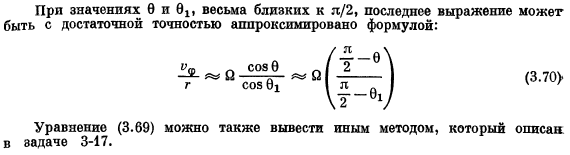
Уравнение (3.42) может быть интегрировано по этим условиям.если r= xH, то скорость » в результате кг Я — » 2 М = 2lHL (- Бев)| оружие = 4lRYOoO2) Рисунки 3-5.Вращающаяся жидкость со свободной поверхностью в виде вращающейся параболы. (3.49) Формула (3.49) Сразу. (3.50)) (3.51) Где C и C-интегральные константы.
Значение cw не может быть бесконечно большим при r = 0, поэтому константа Cr = 0.in в случае r-H, кроме того, известно, что компонент скорости равен DO.Отсюда вы можете найти значение Cr и получить его. чч = ОГ (3.52) д-р ДТ (3.53) = па = Р (3.54) (3.55) Р = — РГ +uro2′, 2+ с (3.56) По = — Р8 ’+ С pO2g2 Р-Ро = — Пэ («- «О) Ч-2— Свободная поверхность-это геометрическое место (3.60)) (3.61 а> 6 ингредиентов (3.61 б> 4-2s1ge ^ 1 Теперь предположим, что он настолько медленный, насколько это возможно.
Смотрите также:

